【深度学习】深度学习基础知识笔记

1 激活函数

1.1 Sigmoid 函数

数学公式：

\[ S(x)=\frac{1}{1 + e^{-x}}=\frac{e^x}{e^x+1}=1-S(-x) \]

调用示例：

torch.sigmoid(torch.tensor([1.0, 2.0, 3.0], device='cuda:0'))
nn.Sigmoid(inplace=True)

图像：

Sigmoid

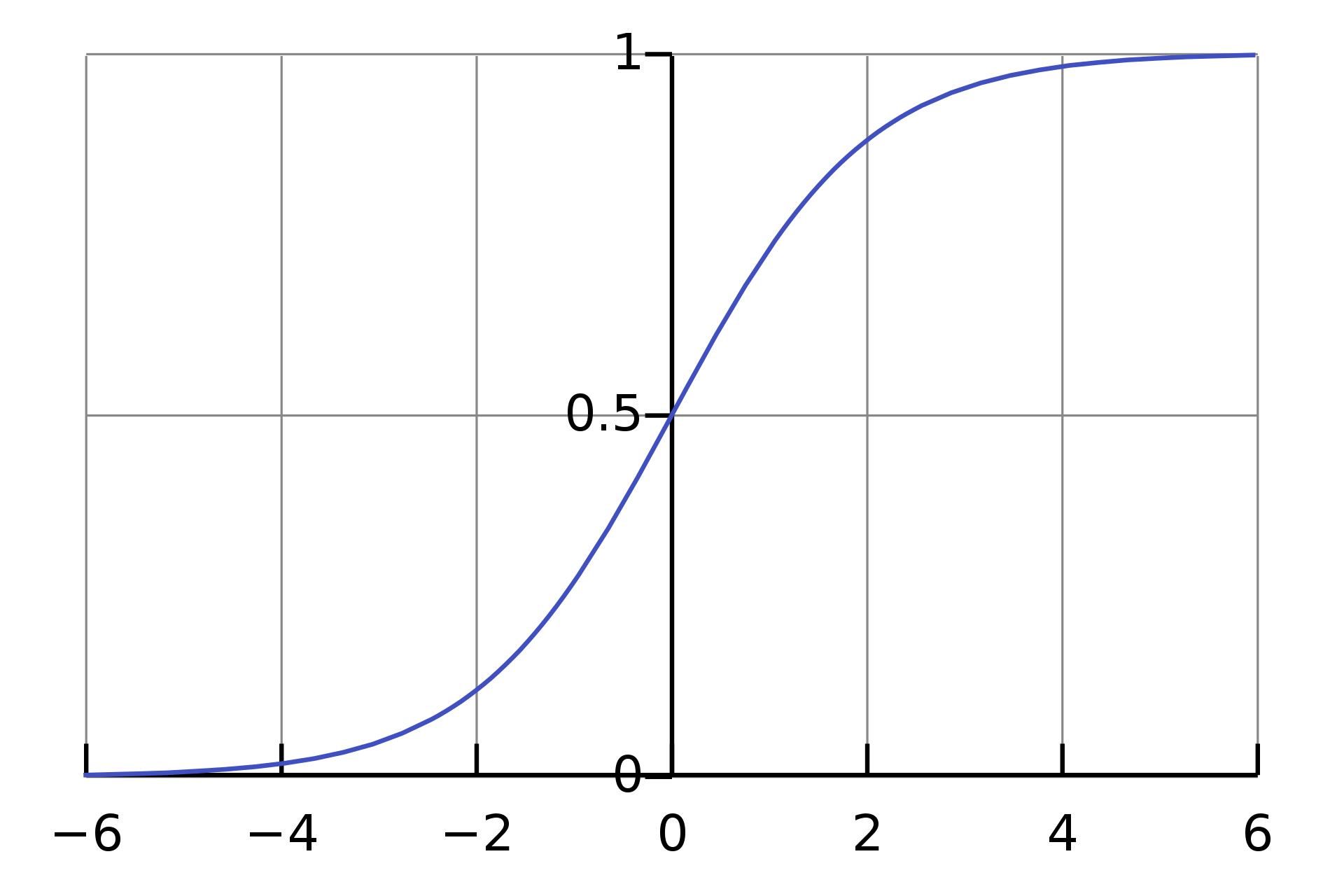
介绍：

• 优点：
  • 非线性变换
  • 二分类问题
  • 易于计算梯度，进行反向传播
• 缺点：
  • 输入值较为极端时，容易出现梯度消失（梯度=0），影响训练效果
  • 指数运算较慢

1.2 ReLU 函数

数学公式：

\[ R(x)=max(0,x) \]

调用示例：

torch.relu(torch.tensor([1.0, 2.0, 3.0], device='cuda:0'))
nn.ReLU(inplace=True)

图像：

介绍：

线性单元

1.3 Leaky ReLU 函数

数学公式：

\[ f(x)=\begin{array}{l} \left\{\begin{matrix} x,x\ge0\\ ax,x<0 \\ \end{matrix}\right. \end{array} \]

其中a常取0.01~0.3

调用示例：

nn.LeakyReLU()

图像：

介绍：

线性修正单元

1.4 Softmax 函数

数学公式：

\[ S(\vec{z_{i}})=\frac{e^{\vec{z_{i}}}}{\sum_{j=1}^{n}e^{\vec{z_{j}}}}\quad{(i=1,2,3,\dots ,n)} \]

调用示例：

nn.Softmax()

图像：

介绍：

1.5 GELU 函数

数学公式：

\[ \begin{aligned} \text{高斯误差线性单元:}&\quad\operatorname{GELU}(x)=\frac{x}{2}(1+\text{erf}(\frac{x}{\sqrt{2}})) \\ \text{高斯误差函数:}&\quad\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x} e^{-t^2}dt \end{aligned} \]

其中 erf() 函数无法求原函数，需要采用数值积分进行计算。

近似计算方法： \[ \quad\operatorname{GELU}(x)=\frac{x}{2} \cdot \left(1 + \operatorname{tanh}\left(\sqrt{\frac{2}{\pi}} \cdot (x + 0.044715 \cdot x^3)\right)\right) \] 近似方法来自论文：

Gaussian Error Linear Units (GELUs)

调用示例：

nn.GELU()

图像：

介绍：

高斯误差线性单元（Gaussian Error Linear Units）