【算法】【希尔排序】算法与代码、实例讲解

希尔排序是一种改进的插入排序算法，也称为缩小增量排序。它通过将数组分为多个子序列来进行排序，然后逐步缩小子序列的间隔，最终将整个数组变为一个有序序列。希尔排序的关键是选择适当的间隔序列。

希尔排序的算法步骤如下：

1. 选择一个间隔序列，也称为增量序列（increment sequence），用于划分子序列。
2. 对于每个增量值，从当前增量开始，对子序列进行插入排序。
3. 逐步缩小增量，重复步骤2，直到增量为1。
4. 最后，进行一次增量为1的插入排序，完成排序。

由于经过希尔排序后的数组更加有序，因此插入排序所需的swap量减少，性能提高，这是希尔排序的改进。

insertionSort

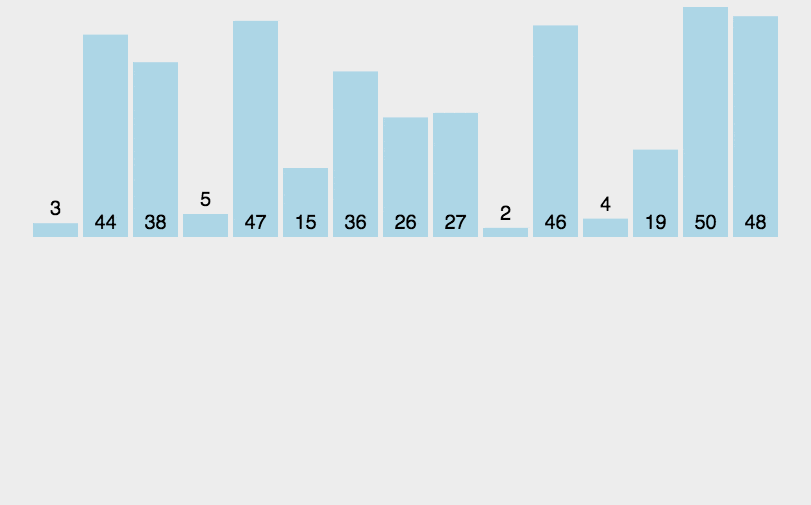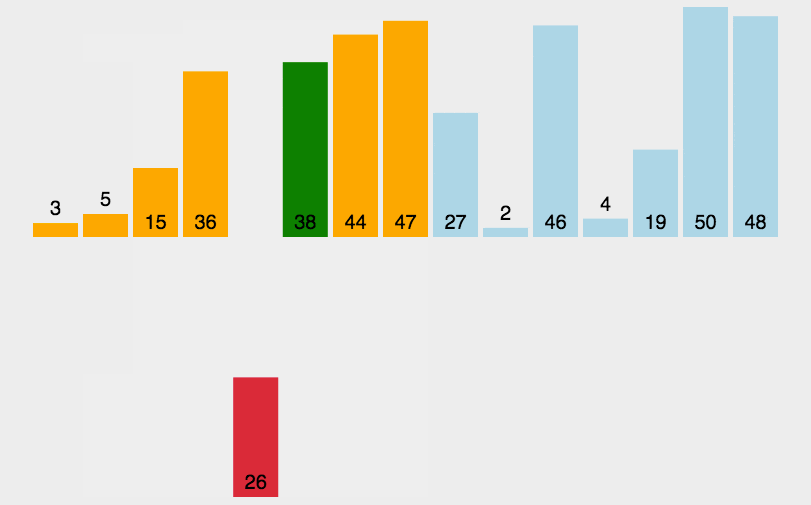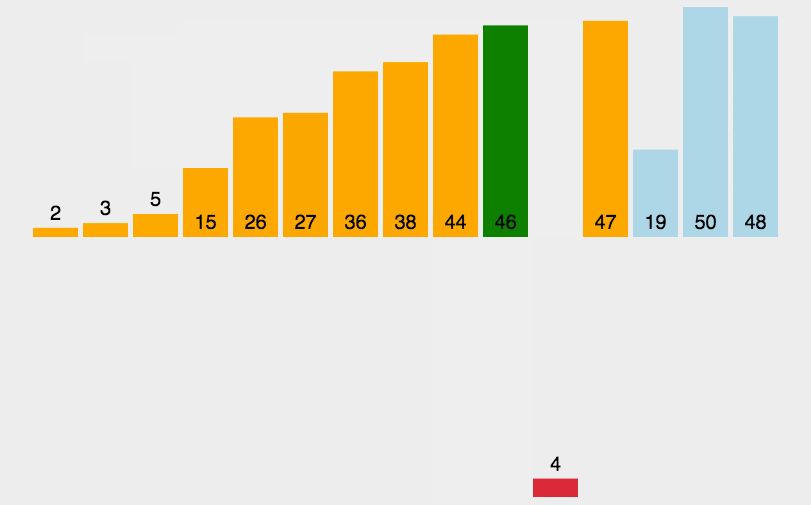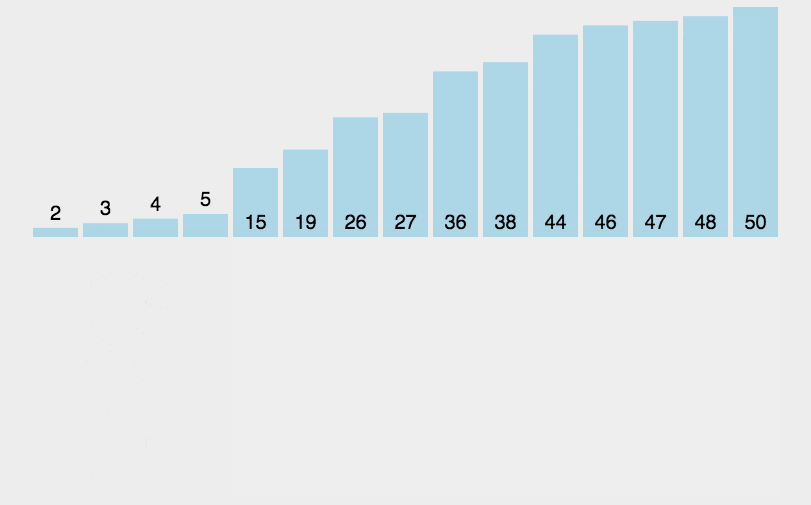
现在让我们来看一下带有注释的C++代码示例：

#include <iostream>
using namespace std;

// 带有增量的插入排序
void insertSort(int arr[], int n, int gap) {
    for (int i = gap; i < n; i++) {
        int temp = arr[i];
        int j = i;

        // 对子序列进行插入排序
        while (j >= gap && arr[j - gap] > temp) {
            arr[j] = arr[j - gap];
            j -= gap;
        }

        arr[j] = temp;
    }
}

// 希尔排序函数
void shellSort(int arr[], int n) {
    // 定义增量序列，常用的增量序列选择是希尔增量（Shell's increment）
    int gap = n / 2;
    // 逐步缩小增量直到1
    while (gap > 0) {
        // 对每个子序列进行插入排序
        insertSort(arr, n, gap);
        // 缩小增量
        gap /= 2;
    }
}

// 测试希尔排序
int main() {
    int arr[] = { 9, 5, 1, 4, 3, 8, 6, 2, 7 };
    int n = sizeof(arr) / sizeof(arr[0]);

    cout << "原始数组：";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;

    shellSort(arr, n);

    cout << "排序后数组：";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;

    return 0;
}

以数组 {4, 2, 1, 3, 6, 5, 8, 7} 为例，详细讲解希尔排序的过程：

Step 1:

初始数组: 4 2 1 3 6 5 8 7

选择希尔增量（间隔）gap = 8 / 2 = 4

将数组划分为四个子序列：

子序列1: 4 6

子序列2: 2 5

子序列3: 1 8

子序列4: 3 7

对每个子序列进行插入排序：

子序列1: 4 6 （已排序）

子序列2: 2 5 （已排序）

子序列3: 1 8 （已排序）

子序列4: 3 7 （已排序）

合并子序列得到中间结果：

4 2 1 3 6 5 8 7

Step 2:

缩小增量，gap = 4 / 2 = 2

将数组划分为两个子序列：

子序列1: 4 1 6 8

子序列2: 2 3 5 7

对每个子序列进行插入排序：

子序列1: 1 4 6 8 （已排序）

子序列2: 2 3 5 7 （已排序）

合并子序列得到中间结果：

1 2 4 3 6 5 8 7

Step 3:

缩小增量，gap = 2 / 2 = 1

将整个数组作为一个子序列进行插入排序：

子序列: 1 2 4 3 6 5 8 7

插入排序后得到最终结果：

1 2 3 4 5 6 7 8

通过希尔排序算法的多次迭代和插入排序，我们成功将原始数组 {4, 2, 1, 3, 6, 5, 8, 7} 排序为 {1, 2, 3, 4, 5, 6, 7, 8}。在每个步骤中，希尔排序算法根据指定的增量（间隔）将数组划分为子序列，并对每个子序列进行插入排序。随着增量的不断缩小，最终完成整个数组的排序。