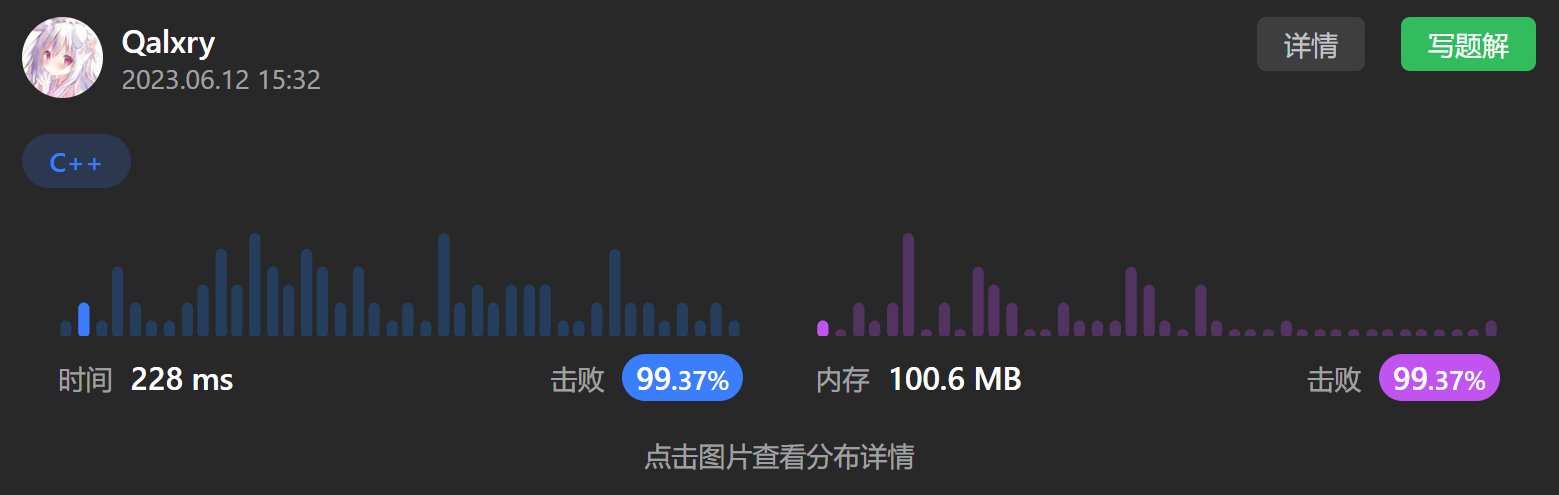
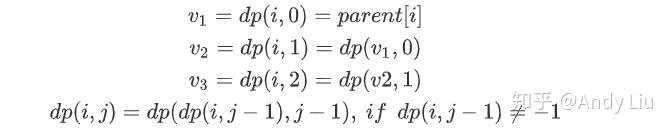本文最后更新于:2023年9月5日 中午 12:13
文章转载自知乎Andy Liu leetcode第193周赛第四题树节点的第
K 个祖先
leetcode1483. 树节点的第 K
个祖先
给你一棵树,树上有 n 个节点,按从 0 到
n-1 编号。树以父节点数组的形式给出,其中
parent[i] 是节点 i
的父节点。树的根节点是编号为 0 的节点。
请你设计并实现 getKthAncestor``(int node, int k)
函数,函数返回节点 node 的第 k
个祖先节点。如果不存在这样的祖先节点,返回 -1 。
树节点的第 k
个祖先节点是从该节点到根节点路径上的第 k 个节点。
示例:
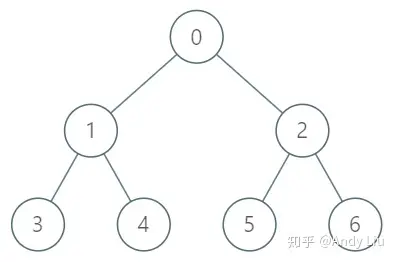
输入:
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]
输出:
[null,1,0,-1]
解释:
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // 返回 1 ,它是 3 的父节点
treeAncestor.getKthAncestor(5, 2); // 返回 0 ,它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点
提示:
- 1 <= k <= n <= 5 *10^4
- parent[0] == -1 表示编号为 0 的节点是根节点。
- 对于所有的 0 < i < n ,0 <= parent[i] < n
总成立
- 0 <= node < n
- 至多查询 5 *10^4 次
方法:动态规划dp+binary
lifting倍增
思路:
这道题容易想到的暴力方法就是,对给定的node,进行k次往上查找。这种情况下,每次查找需要运算k次,如果n次查找需要kn次,根据数据范围,时间复杂度会达到O(n^2)。对于数据范围n=50000来说会超时。
我们这里来进行优化,使用动态规划dp+binary
lifting倍增。这个倍增的方法好像是ACM竞赛算法,怪不得我根本想不到,这次就是学习了。
我们主要优化的就是查找的过程,使查找的复杂度从O(n)降低到O(logn)。我们使用动态规划,dp(i,j)表示结点i向上找
2 ^ j次之后的结点,如果超过根节点了,不满足,那么就是-1。这里面j表示2 ^
j次,这就是倍增(binary
lifting)。我们根据数据范围,可知道j最大可取到15。
下面考虑状态转移方程。我们从0开始,dp(i,0)就表示i结点向上找1次的结点,也就是parent[i]:
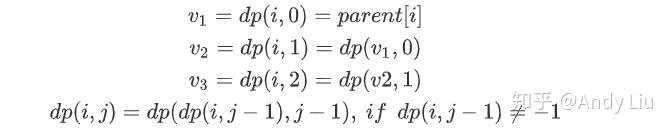
最后一个等式即为状态转移方程,i的2 ^
k次向上查找,就分成了先将i进行 2^ k-1次查找,再对结果进行 2^
k-1次查找,如果前2^
k-1次查找已经越过了根节点,那么就跳过,dp(i,j)=-1。
可以看到,状态转移方程中,与j-1有关,所以我们外层循环为j,内层循环为i,初始条件为dp(i,0)=parent[i]。
我们查找的时候如何进行呢?
我们从低到高对查找次数k的二进制每一位进行判断,如果该位i为1,那么就说明它需要向上查找2
^ i次,即node = dp[node]
[i],遍历i从0到15,不断更新node,node为-1时,直接返回-1,最后返回node即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class TreeAncestor:
def __init__(self, n: int, parent: List[int]):
self.dp = [[-1for _ in range(16)] for _ in range(n)]
for i in range(n):
self.dp[i][0] = parent[i]
for j in range(1,16):
for i in range(n):
if self.dp[i][j-1] != -1:
self.dp[i][j] = self.dp[self.dp[i][j-1]][j-1]
def getKthAncestor(self, node: int, k: int) -> int:
for i in range(16):
if k & (1<<i):
if node >= 0:
node = self.dp[node][i]
else:
return -1
return node
|
结果:
我的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class TreeAncestor {
private:
vector<vector<int>> dp;
public:
TreeAncestor(int n, vector<int>& parent) {
dp.resize(n, vector<int>(16, -1));
for (int i = 0; i < n; i++)
dp[i][0] = parent[i];
for (int j = 1; j < 16; j++) {
for (int i = 0; i < n; i++) {
if (dp[i][j-1] != -1) {
dp[i][j] = dp[dp[i][j-1]][j-1];
}
}
}
}
int getKthAncestor(int node, int k) {
for (int i = 0; i < 16; i++) {
if (k & (1 << i)) {
if (node >= 0) {
node = dp[node][i];
} else {
return -1;
}
}
}
return node;
}
};
|
更快的两个版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class TreeAncestor {
private:
vector<vector<int>> dp;
public:
TreeAncestor(int n, vector<int>& parent) {
dp.resize(n, vector<int>(16, -1));
for(int i = 0; i < n; i++)
dp[i][0] = parent[i];
for(int i = 0; i < n; i++)
for(int j = 1; j < 16 && dp[i][j-1] != -1; j++)
dp[i][j] = dp[dp[i][j-1]][j-1];
}
int getKthAncestor(int node, int k) {
for(int i = 0; k && node != -1; k >>= 1, i++)
if(k & 1) node = dp[node][i];
return node;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
int dp[50002][16];
class TreeAncestor {
private:
public:
TreeAncestor(int n, vector<int>& parent) {
n++;
for(int i = 1; i < n; i++)
dp[i][0] = parent[i-1] + 1;
for(int i = 2; i < n; i++)
for(int j = 1; j < 16 && dp[i][j-1]; j++)
dp[i][j] = dp[dp[i][j-1]][j-1];
}
int getKthAncestor(int node, int k) {
node++;
for(int i = 0; k && node; k >>= 1, i++)
if(k & 1) node = dp[node][i];
return node - 1;
}
};
|