【算法】【大数】计算k的10000次方的前10位数字

计算 k 的 10000 次方的前 10 位数字

根据公式： \[ \begin{align} k^{10000} &= 10^{10000\times \log_{10}k} \\ &= 10^{float+\lfloor10000\times \log_{10}k\rfloor} \\ &= 10^{float} \times 10^{\lfloor10000\times \log_{10}k\rfloor} \end{align} \] 计算 \(10^{float}\) ，然后获取其前10位有效数字即可。注意 \(k^{10000}\) 只有 \(\lfloor10000\times \log_{10}k\rfloor + 1\) 位数字。

例：

---

计算 \(2^{20}\) 的前7位数字： \[ \begin{align} 2^{20} &= 10^{20\times \lg{2}} \\ &= 10^{6.02059991327...} \\ &= 10^{0.02059991327...} \times 10^{6} \\ &= 1.048575999999... \times 10^6 \\ &= 1.048576 \times 10^6 \end{align} \] 结果为：1048576.

---

计算 \(2^{10000}\) 的前10位数字： \[ \begin{align} 2^{10000} &= 10^{10000\times \lg{2}} \\ &= 10^{3010.2999566398...} \\ &= 10^{0.2999566398...} \times 10^{3010} \\ &= 1.995063116... \times 10^{3010} \end{align} \] 结果为1995063116.

使用nodejs验证：

NodeJS的BigInt计算

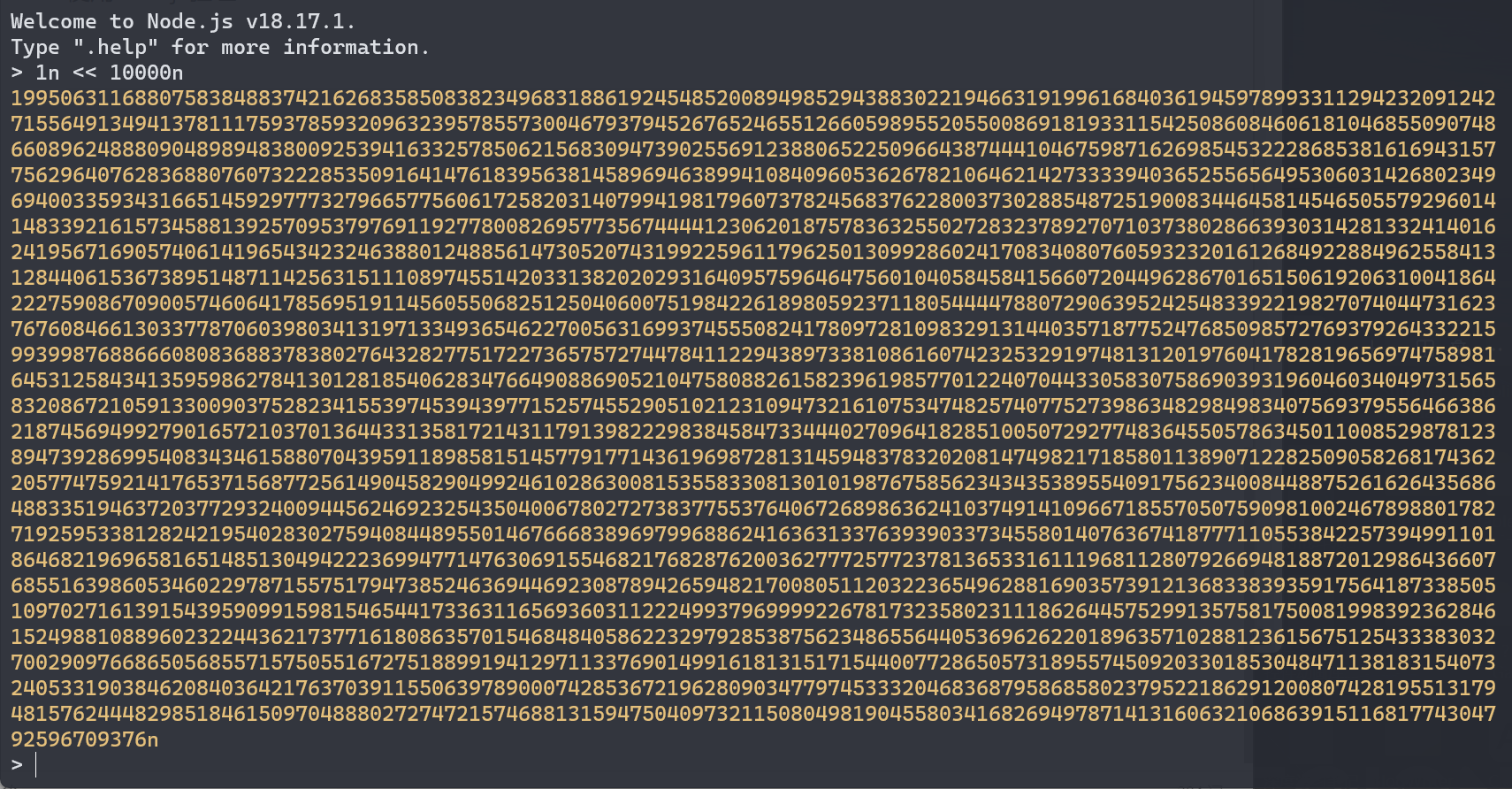
其前10位精度在使用double情况下尚可。

Node和Python的精度

---