本文最后更新于：2024年4月13日晚上 21:01

DP优化总结

0 基本概念
- 1D/1D 方程
- 2D/1D 方程
1 (1D/1D) 单调队列优化
2 (1D/1D) 斜率/凸壳优化
3 (1D/1D) 决策单调性优化
4 (2D/1D) 四边形不等式优化
5 (2D/1D) WQS带权二分优化
6 (2D/0D) 矩阵乘法优化
7 (1D/1D) 闵可夫斯基和优化
- 概述
- 算法流程
- 优化 DP
- 例题
- 参考资料
8 (1D/1D) Slope Trick
- 概述
- 例题
9 (xD/yD) 数据结构优化

0 基本概念

我们对DP的状态转移方程按照状态维度和决策点维度（转移点维度），分为 1D/1D 和 2D/1D 。

1D/1D 方程

1D/1D 方程，意思是我们计算的 $dp[i]$ 的状态维度是 1 维的 $[i]$ ，决策点的维度是 1 维的 $[j]$ 。

状态转移方程：

\[ \begin{align} f(i)&=\min/\max\limits_{}\{g(j)+w(i,j)\},\quad 1\le j < i \end{align} \]

我们按照 $w(i,j)$ 的性质继续细分：

(1) $w(i,j)$ 为多项式函数

a. $w(i,j)$ 为一次函数：单调队列优化

b. $w(i,j)$ 为高次函数：斜率/凸壳优化

其中根据 $w(i,j)$ 的情况，有不同的优化策略：

单调队列

二分队列

动态凸包：CDQ分治、线段树维护、李超线段树

(2) $w(i,j)$ 为非多项式函数

a. $w(i,j)$ 满足四边形不等式：决策单调性优化

其中根据 $w(i,j)$ 的单调性，有不同的优化策略：

单调队列（有单调性）

二分队列（无单调性）

CDQ分治（无单调性）

2D/1D 方程

2D/1D 方程，意思是我们计算的 $dp[i][j]$ 的状态维度是 2 维的 $[i][j]$ ，决策点的维度是 1 维的 $[k]$ 。

状态转移方程：

\[ \begin{align} f(i,j) &= \min/\max\{g(i,k)+h(k,j)+w(i,j)\},\quad k \in [i,j-1] \end{align} \]

如果决策点 $[k]=[j]$ ，则状态转移方程：

\[ f(i,j) = \min/\max\{g(i,j)+w(i,j)\},\quad j \in [1,i] \]

我们继续细分：

(1) $f(i,j)$ 具有凸性

WQS带权二分

(2) $w(i,j)$ 满足四边形不等式

四边形不等式优化（区间决策单调性）

1 (1D/1D) 单调队列优化

概念

(1) $ds[j]$ 与 $i$ 无关：单调队列

单调队列优化特征状态方程：

\[ \begin{align} dp[i]&=\min/\max\{dp[j]+a[i]+b[j]\}, \quad j \in[L(i),R(i)] \\ &=\min/\max\{dp[j]+b[j]\} +a[i] \\ \end{align} \]

设 $ds[j]= dp[j]+b[j]$，其中 $ds[j]$ 的计算与 $i$ 完全无关。可得：

\[ dp[i]=\min/\max\{ds[j]\} +a[i], \quad j \in[L(i),R(i)] \]

由于 $ds[j]$ 仅和 $j$ 有关，与 $i$ 无关，故 $ds[j]$ 仅需计算一次即可用于全部 $dp[i]$ 的计算中。

未优化前，在每一轮 $i$ 的循环中都要计算一遍 $\min/\max\{ds[j]\}，j \in[L(i),R(i)]$ ，期间有大量重复的 $ds[j]$ 计算。故考虑用单调队列存储 $\min/\max\{ds[j]\}，j \in[L(i),R(i)]$ 。单调队列可用于数组上的滑动窗口，此处 $j \in[L(i),R(i)]$ 也是一个滑动窗口，求滑动窗口内的最值。

我们可在遍历 $i$ 的同时计算当前的 $\min/\max\{ds[j]\}，j\in [R(i-1)+1,R(i)]$ ，将当前计算出的值逐个压入单调队列。

如果是当前的最值，就将前面计算的值全部弹走，队首为该最值
如果不是当前的最值，压入队尾，作为未来可能的最值。
检查队首的值是否在滑动窗口范围外，将 $ds[j]，j\in [1，R(i-1)]$ 弹出队首。

实际中，单调队列储存的值为 $ds$ 的下标 $j$， $ds[j]= dp[j]+b[j]$ 可以不额外存储。

请注意： $ds[j]$ 的计算必须完全与 $i$ 无关！

(2) $ds[j]$ 与 $i$ 有关：二分单调栈

如上面的注解中提到， $ds[j]$ 的计算必须完全与 $i$ 无关。这使得 LIS 问题无法使用单调队列解决。

LIS 问题的通常解法是：设 $dp[i]$ 为前 $i$ 个元素的最长上升子序列长度，则有

\[ dp[i]=\max\{dp[j]\}+1, ~j \in(0,i),~a[j]\le a[i] \]

看似方程符合单调队列优化，但是有 $a[j]\le a[i]$ 的限制条件，这就使得 $dp[j]$ 的计算与 $i$ 有关了，无法使用单调队列优化。朴素的解法是 $O(n^2)$ 的时间复杂度。

我们重新设置状态，令 $dp[i]$ 表示长度为 $i$ 的上升子序列的最后一个元素的最小值，则有：

\[ dp[i]=\min\{dp[j]\}+1, ~j \in[1,i),~dp[j]<a[i] \]

这时候我们考虑每次计算 $dp[i]$ 时都通过二分来搜索 $dp[j]$ 的最大值。

为每个 $dp[j]$ 记录该子序列的最后一个元素的值。
同时若子序列长度相同，则记录最后一个元素是最小的那个。
根据 $a[i]$ 二分搜索 $dp[j]$ ，找到最后一个 $\le a[i]$ 的 $dp[j]$ 。
然后更新 $dp[i]=dp[j]+1$ ，记录 $a[i]$ 为 $dp[i]$ 对应子序列的最后一个元素。

这样的时间复杂度为 $O(n\log n)$ 。

虽然没有人称其为二分单调栈，通常只称为二分解法，但其实个人感觉比较相似，同时为了和斜率优化对应，这里也称为二分单调栈。

单调队列优化模板题

1. 【单调队列】P2627 USACO11OPEN Mowing the Lawn G

题意概述

有一个包括 $n$ 个正整数的序列，第 $i$ 个整数为 $E_i$ ，给定一个整数 $k$ ，找这样的子序列，如果子序列中的数在原序列中连续，则连续长度不能超过 $k$ 。对于子序列求和，问所有子序列中最大的和是多少？

单调队列题解

设 $dp[i]$ 为前 $i$ 个整数的最大子序列和，则状态转移方程为：

\[ dp[i] = \max \{dp[j-1]+sum[i]-sum[j]\},\quad j \in [i-k,i] \]

其中 $sum[i]$ 是前缀和，$sum[i]-sum[j]$ 求的是 $[i-k,i]$ 区间和。

根据单调队列优化：

\[ \begin{align} dp[i] &= \max \{dp[j-1]-sum[j]\}+sum[i],\quad j \in [i-k,i] \\ &=\max \{ds[j]\}+sum[i] \end{align} \]

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100007;
ll n, k, e[N], sum[N], dp[N];
ll ds[N];
// 单调队列，为了简便没有写为循环队列，head
// 由于这里是求最大值，故 ds[q[tail]] < ds[j] 为从队首到队尾的单调递减队列
// 如果是求最小值，则为从队首到队尾的单调递增队列，即 ds[q[tail]] > ds[j]
// q[head] < j - k 为了保证队列中的元素都在滑动窗口[i - k, i] (j == i)内
// head 指向队首元素，tail指向队尾元素，当队中没有元素时，tail = head - 1
int q[N], head = 0, tail = -1;
ll monoQueue(int j) {
    ds[j] = dp[j - 1] - sum[j];
    while (head <= tail && ds[q[tail]] < ds[j])
        tail--;  // ds[j]从队尾进入，经过比它小的值就删去
    q[++tail] = j;
    while (head <= tail && q[head] < j - k)
        head++;
    return ds[q[head]];
}
int main() {
    cin >> n >> k;
    sum[0] = 0;
    for (int i = 1; i <= n; i++) {
        cin >> e[i];
        sum[i] = sum[i - 1] + e[i];
    }
    monoQueue(0);  // 初始化单调队列 ds[0] = dp[-1] - sum[0] = 0 - 0 = 0
    for (int i = 1; i <= n; i++)
        dp[i] = monoQueue(i) + sum[i];
    cout << dp[n];
    return 0;
}

2. 【二分单调栈】

2 (1D/1D) 斜率/凸壳优化

概念

斜率/凸壳优化特征状态方程：

\[ dp[i]=\min \{dp[j]-a[i]d[j]\}, \quad j \in [0,i-1], \quad a[i] \le a[i+1], \quad d[j]\le d[j+1] \]

特点：存在一个既有 $i$ 又有 $j$ 的项 $a[i]d[j]$ ，并且 $a[i]$ 和 $d[j]$ 都是单调不减， $j \in [0,i-1]$ 。

\[ \begin{align} \because dp[i] &= dp[j] - a[i]d[j] \\ \therefore dp[j] &= a[i]d[j] + dp[i] \\ \end{align} \]

\[ 设~y=dp[j],x=d[j],k=a[i],b=dp[i],~得:\\ y=kx+b \]

其中 $b=dp[i]$ 是我们要求的值，并且要是最小值，故最小化 $dp[i]$ 的问题转化为：

对于 $j \in [0,i)$ 中的不同的 $j$ ，会产生一系列点 $(d[j],dp[j])=(x_j,y_j)$ 分布在平面上。
寻找 $(x_j,y_j)$ ，在斜率 $k=a[i]$ 的情况下，能够使截距 $b=dp[i]$ 达到最小值。

通过构造“凸壳”的技巧，我们可以很快寻找到使截距 $b=dp[i]$ 达到最小值的 $(x_j,y_j)$。

我们设这个最优点为 $P_i=(x_j,y_j)$ （下标为 $i$ 表示它是根据 $k=a[i]$ 来寻找的）

这个点一定在下凸壳上，并且它与前一个点的斜率 $\le k$ ，与后一个点的斜率 $\ge k$ （也可能是是凸壳中第一个或最后一个点，当所有线段的斜率都 $\le k$ 或 $\ge k$）。

当我们随着 $i$ 的遍历，计算最新的 $j \in [0,i)$ 对应的 $(x_j,y_j)$ 并加入到平面上时，凸壳上的点会不断更新，以确保它一直是凸壳。比如点 3 在 $i = 3$ 时是最新的点，它与1、2、3组成凸壳，但是当 $i = 4$ 时，随着点 4 的加入，点 3 被排除，1、2、4重新组成凸壳。

Algorithm

凸包构造算法

这种算法为计算几何中一种简单的凸包算法：安德鲁算法（Andrew's Algorithm）

这个是利用单调队列以及斜率的单调性来得到凸包。

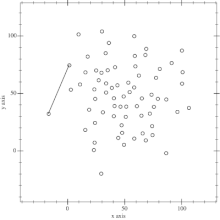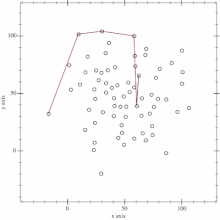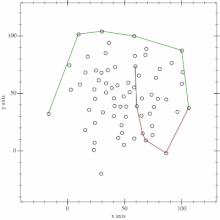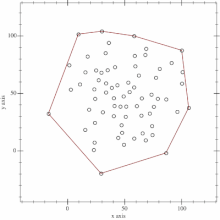
另有别的凸包构建算法：Graham’s Scan

先找到最左下的点（y 最小的最左边的点），计算其他点以该点为原点的极角，并用极角对点进行排序。同样用一个单调队列来维护凸包上的点。

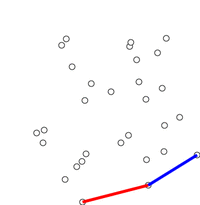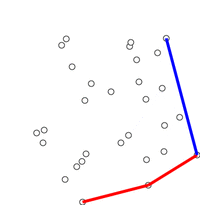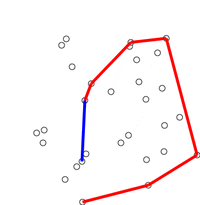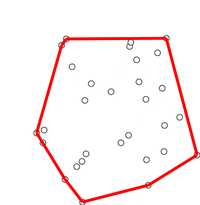
两者时间复杂度受限于排序，为 $O(n\log n)$ 。由于这里给出的 $x=d[j]\le d[j+1]$ ，所以省去了排序的过程。

对于计算 $dp[i] = b_{\min}$ ，我们就在斜率 $k=a[i]$ 的情况下，从左到右遍历凸壳上的点寻找最优 $(x_j,y_j)$ 。该项时间复杂度为 $O(n)$。考虑 $i$ 有 $n$ 次循环，总时间复杂度为 $O(n^2)$。

到目前为止，相较于普通的DP方法，我们仅仅是用凸壳来改进了 $(x_j,y_j)$ 的一部分搜索范围（即只搜索凸壳上的点）。最好情况下是 $(n) $ ，即凸壳上总是只有 1 个点；在最坏情况下，所有点都在凸壳上，时间复杂度为 $(n^2) $

怎么进一步优化呢？

想要优化，那么我们必须要让 $k=a[i]$ 以及 $x=d[j]$ 满足一些性质，让我们能够以优于 $O(n)$ 的时间在凸壳找到最优决策点。最常见的性质为单调性。下面从单调性这一性质展开优化。

斜率优化推导练习

练习1

\[ dp[i]=\min\limits_{j=1}^{i-1}\{a[i]\cdot x[j]+b[i]\cdot y[j]\} + w[i],~其中~x[j],y[j]~可由~dp[j]~在O(1)时间内唯一确定 \]

推导为 $y=kx+b$ 形式：

\[ \begin{align} \frac{dp[i]}{a[i]}&=x[j]+\frac{b[i]}{a[i]}\cdot y[j] + \frac{w[i]}{a[i]}\\ x[j]&=-\frac{b[i]}{a[i]}\cdot y[j]+\left(\frac{dp[i]}{a[i]}-\frac{w[i]}{a[i]}\right)\\ \end{align} \]

(1) $k,x$ 同单调：单调队列

如果最开始给出的特征状态方程还有这样的性质：

\[ a[i] \le a[i+1], \quad d[j]\le d[j+1] \]

$k=a[i]$ 是单调不减的。假设上一轮斜率是 $k_{i-1}$ ，找到了最优点 $P_{i-1}$，下一轮的斜率 $k_i \ge k_{i-1}$，此时凸壳上的最优点 $P_{i}$ 必然在 $P_{i-1}$ 的右侧或它本身。因此凸壳上 $P_{i-1}$ 之前的点不用遍历了，直接跳过。

凸壳上 $P_{i-1}$ 之前的点也可以删除，即使新加入的点使得之前的凸壳发生了变化，我们搜索的起始点也没有变化
$x=d[j]$ 也是单调不减的。说明 $(x_j,y_j)$ 在平面上从左往右是按照 $j$ 从小到大的顺序来分布的。也就是说新加入的点 $(x_j,y_j)$ 只会在最右侧，不会跑到左边破坏我们的凸壳。这样就保证了我们只需要根据凸壳末端的点和新加入的点进行斜率比较即可决定凸壳的更新方式。（与此同时，也支持形成单调队列的结构）

因此，我们只需用单调队列在点一个个被加入时维护凸壳，即可根据上一轮的 $P_{i-1}$ 以 $O(1)$ 找到这一轮的 $P_{i}$ 。

因为每轮只有一个点新加入平面，我们从上一轮的最优点开始往凸壳右边找，很快就能找到。而且最终查询的点数小于凸壳上所有曾经加入的点数。

最终，$i$ 的遍历为 $O(n)$ ，每次寻找 $dp[i] = b_{\min}$ 在凸壳上对应的最优点 $P_{i}$ 的时间为 $O(1)$ ，总时间复杂度为 $O(n)$ 。

思考：如果两者都是单调不增呢？

\[ dp[i]=\min \{dp[j]-a[i]d[j]\}, \quad j \in [0,i-1],\quad a[i] \ge a[i+1], \quad d[j]\ge d[j+1] \]

这样，其实依然是下凸壳，只是从点在平面上的分布来看，遍历顺序（ $[0,i-1]$ ）从原来的【由左到右】变为了【由右到左】而已。我们维护凸壳的时候，要按照斜率递减的方式维护。

斜率/凸壳优化模板代码

for (int i = 1; i <= n; i++) {
    // 删除凸壳上在最优点Pi左边的点，剩下的队列的队首即为最优点Pi
    while (head < tail && slope(q[head], q[head+1]) < k) head++;
    // 根据最优点Pi计算dp[i] = b_min
    int j = q[head];
    dp[i] = ...;
    // 下一轮的点(x_j,y_j)(j = i)加入图中，并更新凸壳（因为j < i，所以这里是下一轮）
    while (head < tail && slope(i, q[tail-1]) < slope(q[tail-1], q[tail])) tail--;
    q[++tail] = i; // 加入队尾
}

上面的代码计算的顺序和前面我们描述的过程不太一样，主要是因为 $0 \le j < i$。

(2) $k$ 不单调，$x$ 单调：二分单调栈

即：

\[ dp[i]=\min \{dp[j]-a[i]d[j]\}, \quad j \in [0,i-1], \quad a[i]~\text{无单调性},\quad d[j]\le d[j+1] \]

$k=a[i]$ 无单调性。这意味着我们无法从上一轮的最优点开始，直接往后在凸壳上找到这一轮的最优点。也就是说，必须搜索当前的整个凸壳！
$x=d[j]$ 单调不减。说明凸壳的维护还是按照（1）中的 Andrew 算法即可，

此时我们必须搜索整个凸壳了，计算凸壳上每两个点构成的直线的斜率。根据（1）中的分析，我们知道，凸壳上的这个“斜率”是单调不减的，对于有序数列的搜索，可以使用二分搜索来优化至 $O(\log n)$ ，我们总共要计算 n 次 $dp[i]$ ，所以总共的时间复杂度为 $O(n\log n)$ 。

因为没有对队首的操作，单调队列成了单调栈。

唯一要注意的就是：凸壳上有多点共线的情况。二分搜索是搜索不到共线的中间的点的，只能搜索到两边的点，并且取哪一边需要看题目的要求如何。

(3) $k$ 单调，$x$ 不单调：动态凸包

即满足：

\[ a[i] \le a[i+1],\quad d[j]~\text{无单调性} \]

$k=a[i]$ 单调不减。受到动态凸包的影响，用不太上，基本可以忽略。每一轮搜索的斜率单调不减，则可以：
- 如果这一轮加入的点未破坏上一轮的最优点，则从上一轮的最优点开始二分
- 如果这一轮加入的点破坏了上一轮的最优点，则从该点开始二分
但实际上这样做只是优化了一点点常数，没什么必要，我们二分的 $\log n$ 已经足够快了。

所以一般忽略这个性质，直接二分即可。
$x=d[j]$ 无单调性。说明凸壳的维护不能使用 Andrew 算法。此时变成了动态凸包问题，考虑使用算法：
- 树状数组、线段树优化：参考最长递增子序列（LIS）问题（$dp[i] = max\{dp[j]\}+1$）。
- 李超线段树
- CDQ分治
- set维护凸包

最终基本上是 $O(n\log n)$ 的时间复杂度。

(4) $k$ 不单调，$x$ 不单调：动态凸包

和（3）的情况几乎一样。

A. 动态凸包：李超线段树

斜率优化模板题

1. 【单调队列】Print Article HDU3507

题意概述

打印一篇有 $N$ 个字的文章，每个字i的打印成本是 $C_i$。此外，在一行中打印 $k$ 个字将花费: $(\sum\limits_{i=1}^{k} C_i)^2 + M$。 $M$ 是一个常数。你的任务是找到一种最佳的打印方式，使得总的打印成本最小。

斜率优化+单调队列解题思路

设 $dp[i]$ 为前 $i$ 个单词的最低成本，$sum[i]$ 为前缀和。

\[ \begin{align*} \because dp[i] &= \min(dp[j] + (sum[i] - sum[j])^2 + M) \\ &= \min(dp[j] + sum[i]^2 - 2 \times sum[i] \times sum[j] + sum[j]^2 + M) \\ \therefore(dp[i] - sum[i]^2) &= \min(dp[j] + sum[j]^2 - 2 \times sum[i] \times sum[j]) + M \\ &= (dp[j] + sum[j]^2) - (2 \times sum[i] \times sum[j]) + M \\ \therefore(dp[j] + sum[j]^2) &= (2 \times sum[i] \times sum[j]) + (dp[i] - sum[i]^2) - M \\ \end{align*} \]

\[ 设~ y = dp[j] + sum[j]^2,~ x = sum[j],~ k = 2 \times sum[i],~ b = dp[i] - sum[i]^2 - m,~则有： \]

\[ y=kx+b \]

$x=sum[j]$ 和 $k=2\times sum[i]$ 都是单调不减，满足斜率优化的要求。

#include <bits/stdc++.h>
using namespace std;
const int N = 500007;
int n, m, c[N], sum[N], dp[N];  // dp[i] 表示前 i 个字的最小打印成本
int q[N], head, tail;
#define K(p) (2 * sum[i])
#define X(p) (sum[p])
#define Y(p) (dp[p] + sum[p] * sum[p])
#define B(p) (dp[i] - sum[i] * sum[i] - m)
// le -> less or equal (<=) , ge -> greater or equal (>=)
// lt -> less than (<) , gt -> greater than (>)
// 以下两行可以避免除法（除法会有误差和除数为0的情况）
// 一定要注意p1和p2的顺序，p1在p2的右边，即p1的x坐标大于p2的x坐标，否则斜率算的是反的
#define slope_le_k(p1, p2 ,k) ((Y(p1) - Y(p2)) <= (X(p1) - X(p2)) * (k))
#define k1_le_k2(p1, p2, p3, p4) ((Y(p1) - Y(p2)) * (X(p3) - X(p4)) <= (Y(p3) - Y(p4)) * (X(p1) - X(p2)))
int main() {
    while (cin >> n >> m) {
        dp[0] = 0;
        sum[0] = 0;
        for (int i = 1; i <= n; i++) {
            cin >> c[i];
            sum[i] = sum[i - 1] + c[i];
        }
        head = 1, tail = 1; // 初始化单调队列: 放入一个元素0 (也抛弃了q[0]，选择下标从1开始)
        q[tail] = 0;        // 这里是 j == 0的情况，只有一个点，所以不需要判断斜率直接放入
        for (int i = 1; i <= n; i++) {
            // 这里不能是 head <= tail ！！！因为至少要有两个元素才能计算斜率
            // 并且也可能是特殊情况：当所有线段的斜率都 <= k 时，此时队列必须剩下一个元素
            // 注意q[head + 1], q[head]的顺序，确保斜率不要反了！！！
            while (head < tail && slope_le_k(q[head + 1], q[head], K(i))) head++;   
            int j = q[head];    // 队首的 j 是最优决策点
            dp[i] = dp[j] + (sum[i] - sum[j]) * (sum[i] - sum[j]) + m;  // 计算 dp[i]
            // 下一轮的点(x_j,y_j)(j = i)加入图中，并更新凸壳（因为j < i，所以这里是下一轮）
            // 由于队列中的点都是凸包上的点，所以这里只需要判断队尾的点是否在凸包外即可
            while (head < tail && k1_le_k2(q[tail], i, q[tail - 1], q[tail])) tail--;
            q[++tail] = i;
        }
        cout << dp[n] << endl;
    }
    return 0;
}

2. 【二分单调栈】

3. 【动态凸包】

3 (1D/1D) 决策单调性优化

概念

决策单调性适用于 1D/1D 方程，意思是我们计算的 $dp[i]$ 的状态维度是 1 维的 $[i]$ ，决策点的维度是 1 维的 $[j]$ 。

特征状态转移方程

\[ f(i)=\min\limits_{1\le j < i}\{g(j)+w(i,j)\} \]

若 $w(i,j)$ 满足四边形不等式：

\[ \begin{align} w(a,c)+w(b,d)&\le w(a,d)+w(b,c),\quad a\le b\le c\le d \\ 或~w(i,j)+w(i+1,j+1)&\le w(i,j+1)+w(i+1,j),\quad i<i+1\le j <j+1 \end{align} \]

则可以进行决策单调性优化。

注1

反四边形不等式的情况如下

\[ f(i)=\max\limits_{1\le j < i}\{g(j)+w(i,j)\} \]

若 $w(i,j)$ 满足反四边形不等式：

\[ \begin{align} w(a,c)+w(b,d)&\ge w(a,d)+w(b,c),\quad a\le b\le c\le d \\ 或~w(i,j)+w(i+1,j+1)&\ge w(i,j+1)+w(i+1,j),\quad i<i+1\le j <j+1 \end{align} \]

则可以进行决策单调性优化。

注2

其实四边形不等式也涵盖了 $g(j)$ ，只不过它在不等式中会被抵消，所以 $w(i,j)$ 起主要作用。

\[ \begin{align} g(j)+w(i,j)+g(j+1)+w(i+1,j+1)&\le g(j+1)+w(i,j+1)+g(j)+w(i+1,j)\\ w(i,j)+w(i+1,j+1)&\le w(i,j+1)+w(i+1,j) \end{align} \]

因此考察函数特性时，可以只看 $w(i,j)$ 的性质。

四边形不等式的性质

将四边形不等式移项变形：

\[ \begin{align} \frac{w(i+\Delta i,j+\Delta j)-w(i,j+\Delta j)}{\Delta i}\le \frac{w(i+\Delta i,j)-w(i,j)}{\Delta i},~\Delta i\to0,~\Delta j\to0 \\ 即~\lim\limits_{\Delta j\to0}\lim\limits_{\Delta i\to0}\frac{w(i+\Delta i,j+\Delta j)-w(i,j+\Delta j)- w(i+\Delta i,j)+w(i,j)}{\Delta j\Delta i}\le0 \tag{1}\\ \frac{w(i+\Delta i,j+\Delta j)-w(i+\Delta i,j)}{\Delta j}\le \frac{w(i,j+\Delta j)-w(i,j)}{\Delta j}, ~\Delta i\to0,~\Delta j\to0 \\ 即~\lim\limits_{\Delta i\to0}\lim\limits_{\Delta j\to0}\frac{w(i+\Delta i,j+\Delta j)-w(i+\Delta i,j)- w(i,j+\Delta j)+w(i,j)}{\Delta i\Delta j}\le0 \tag{2} \end{align} \]

这个其实就是二元函数的混合偏导数的定义了。进一步改写，令 $x=i,~y=j$ ，并重新整理式子，更加直观：

\[ \frac{\partial^2 w}{\partial y\partial x} \le 0,~ \frac{\partial^2 w}{\partial x\partial y} \le 0\\ \]

我超，原来就是混合偏导小于等于零！

我们先来观察有这两个约束条件的连续二元函数的图像具有什么特性：

实际上，如果是连续曲面，则这两个条件相同，由克莱罗定理可得： $\frac{\partial^2 w}{\partial y\partial x}=\frac{\partial^2 w}{\partial x\partial y}$ 。

a. $\frac{\partial^2 w}{\partial y\partial x} \le 0$

从图中可以看到， $0\ge w'(x,y_0) > w'(x,y_0+\Delta)$ 。 $y$ 越大的 $w(x,y_0)$ 的导数越小。

这里我们求取的是最小值。因此 $y$ 更小的 $w(x,y_0)$ 在后面会被 $y$ 更大的 $w(x,y_0+\Delta)$ 反超，并保持一小段的最小优势。形成一个类似于下凸壳的东西。

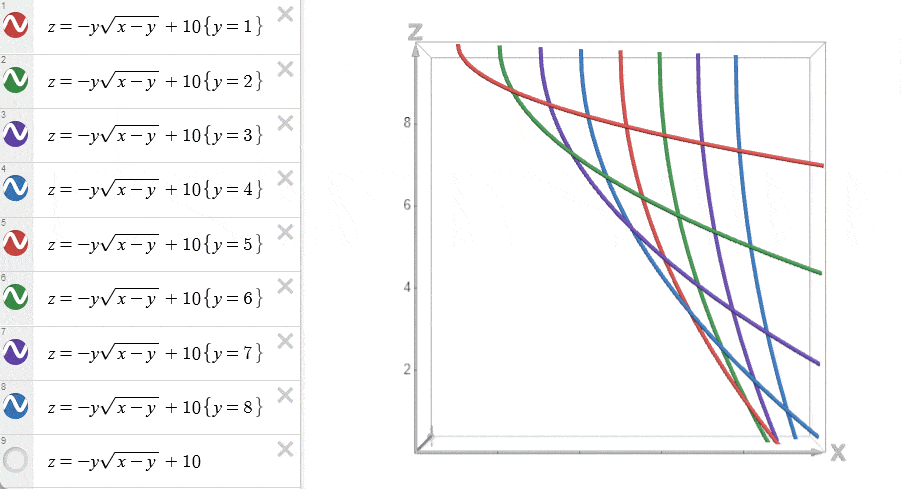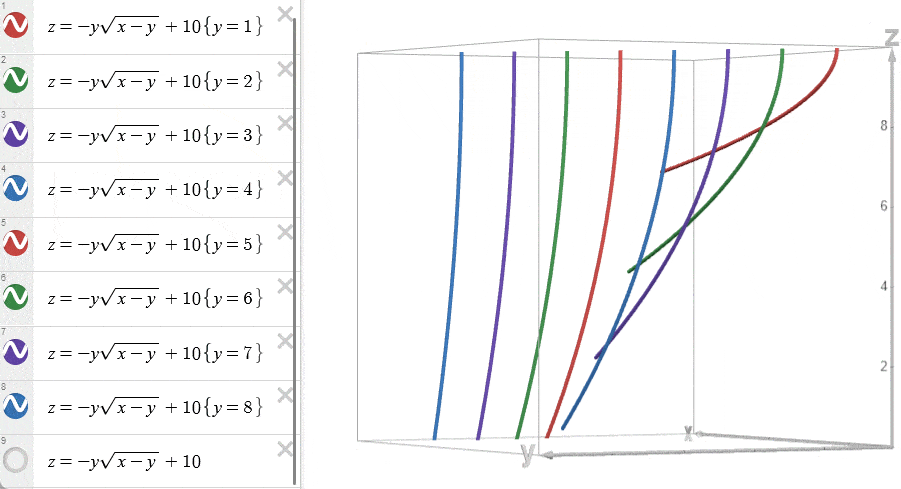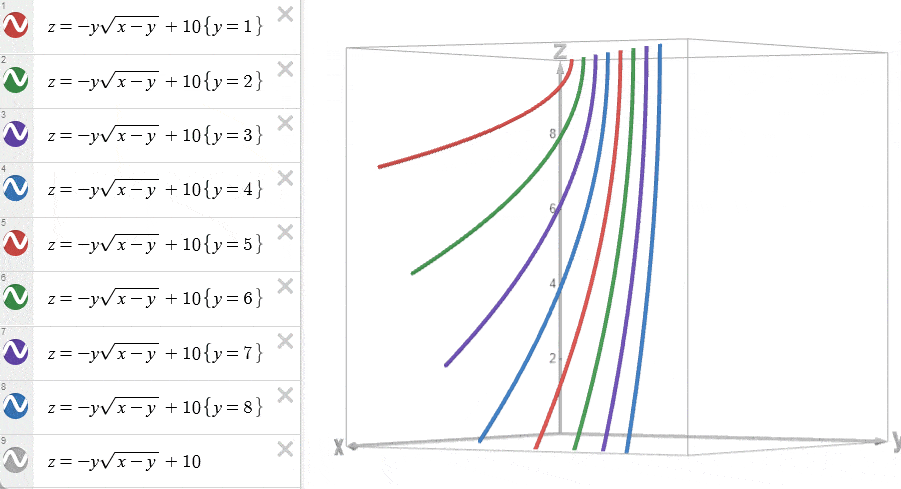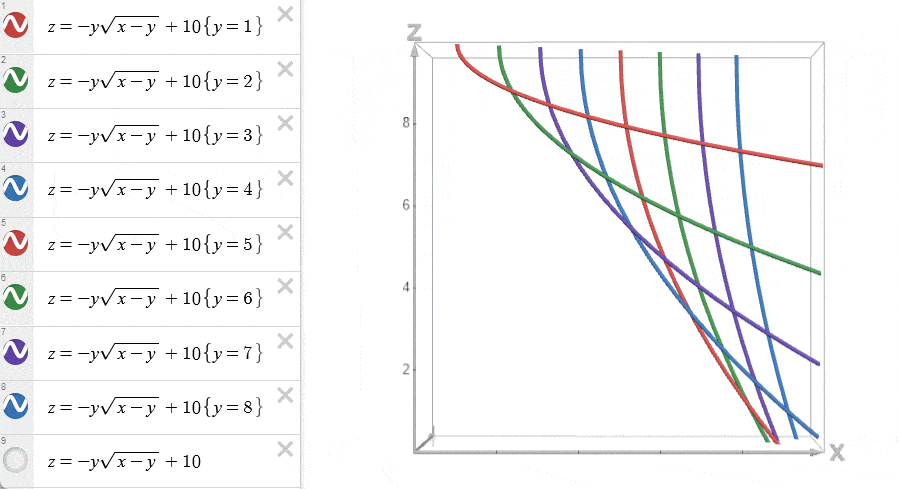
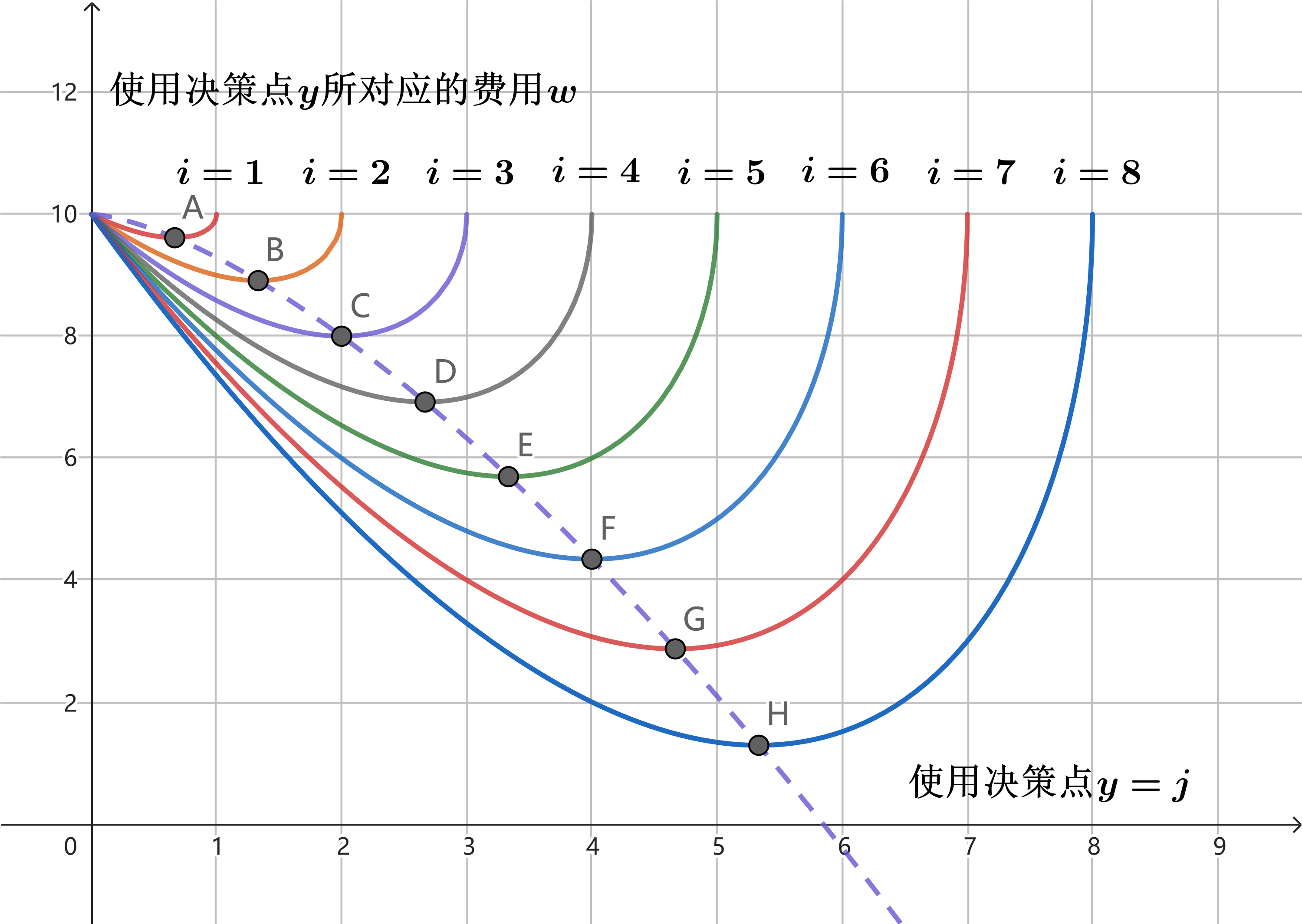
将不同 $y=j$ 的函数 $w(x=i,y=j)$ 绘制在 $w-x$ 平面上。

我们称呼使得 $f(i)$ 取得最优值的 $w(x=i,y=j)$ 为一个决策。由于 DP 计算的是最小值，所以 $f(i)$ 取的是在当前 $x=i$ 下最小费用的决策。

容易发现，在满足四边形不等式的条件下，所取得的决策 $j$ 随 $i$ 的增大而单调不减。故称为决策单调性。

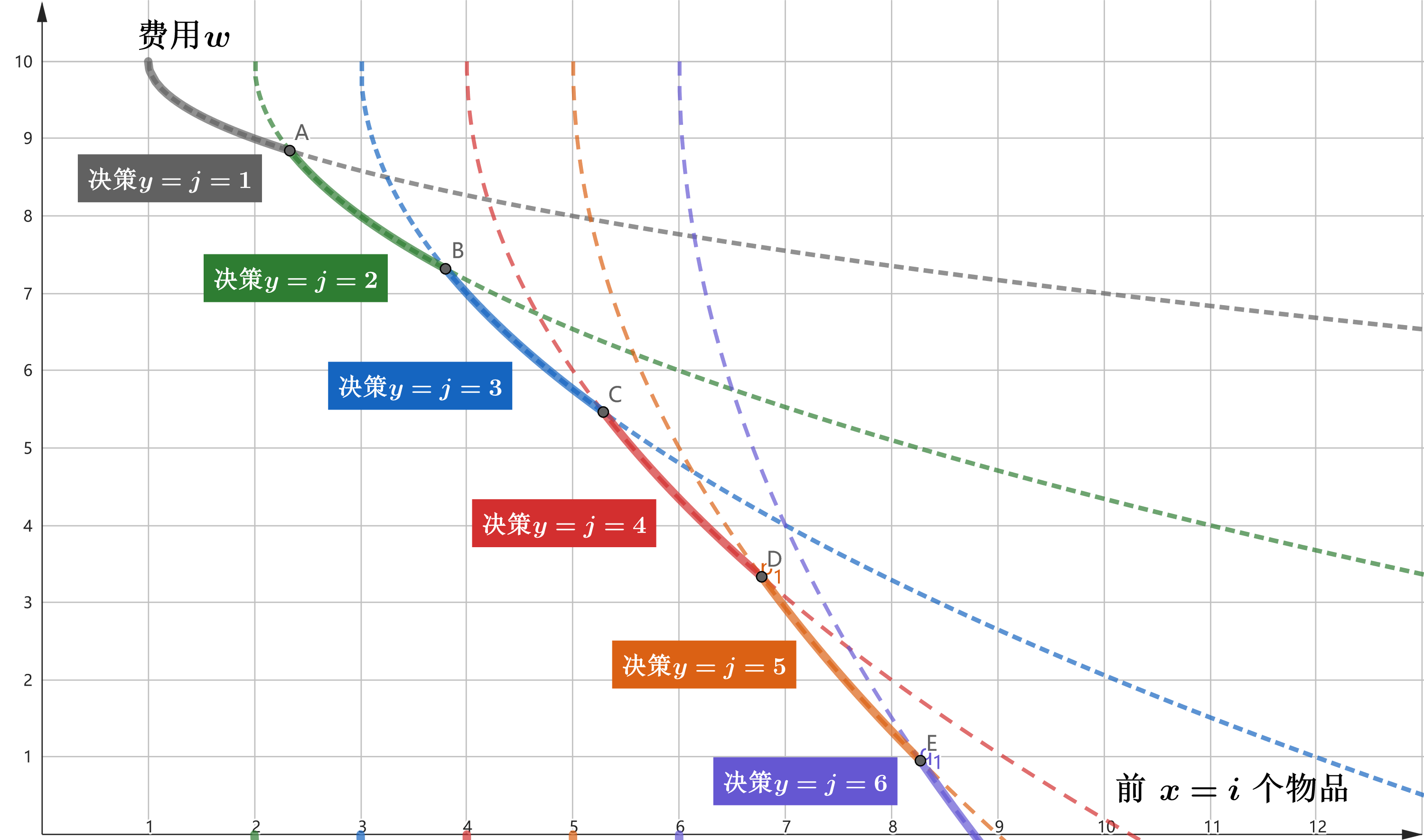
b. $\frac{\partial^2 w}{\partial x\partial y} \le 0$

再来看看酷炫的3D动画吧~

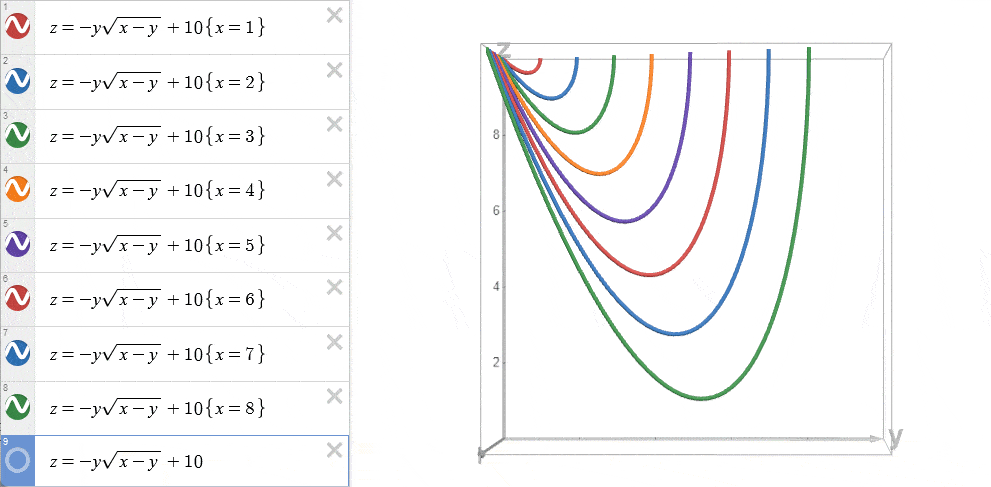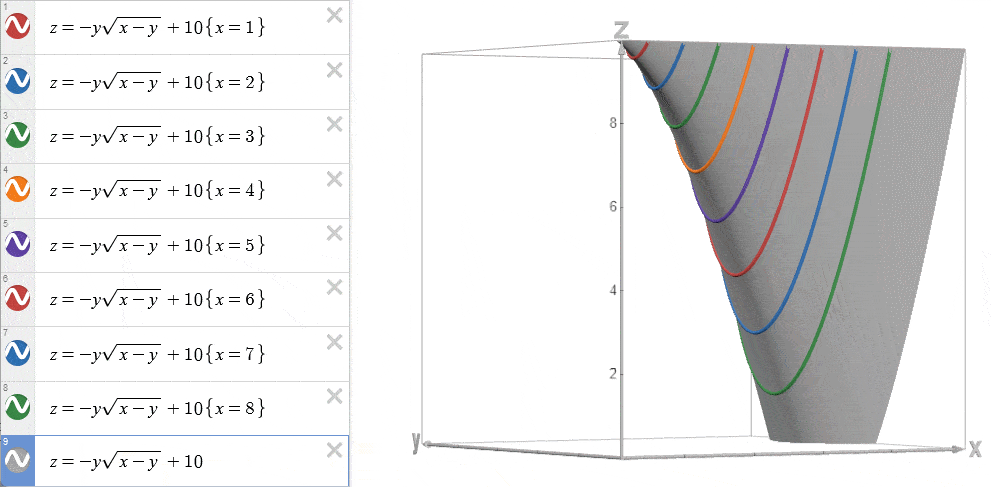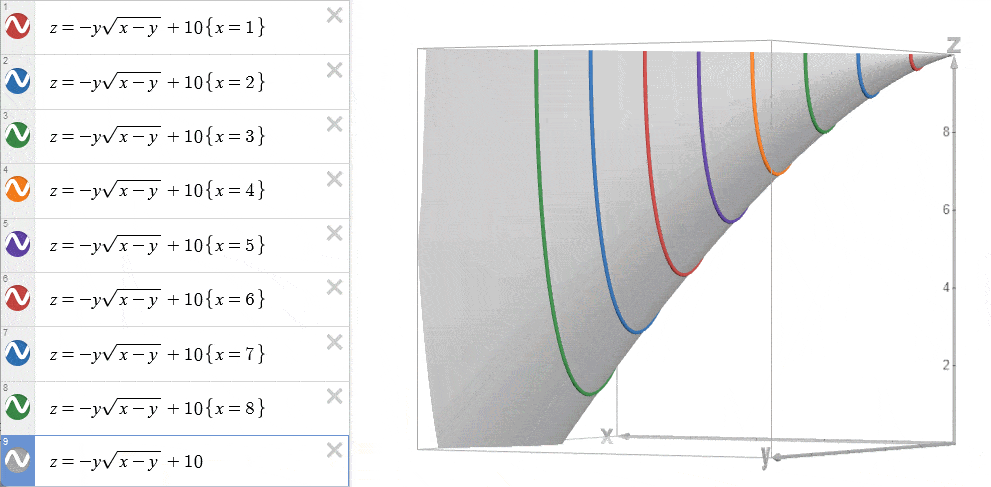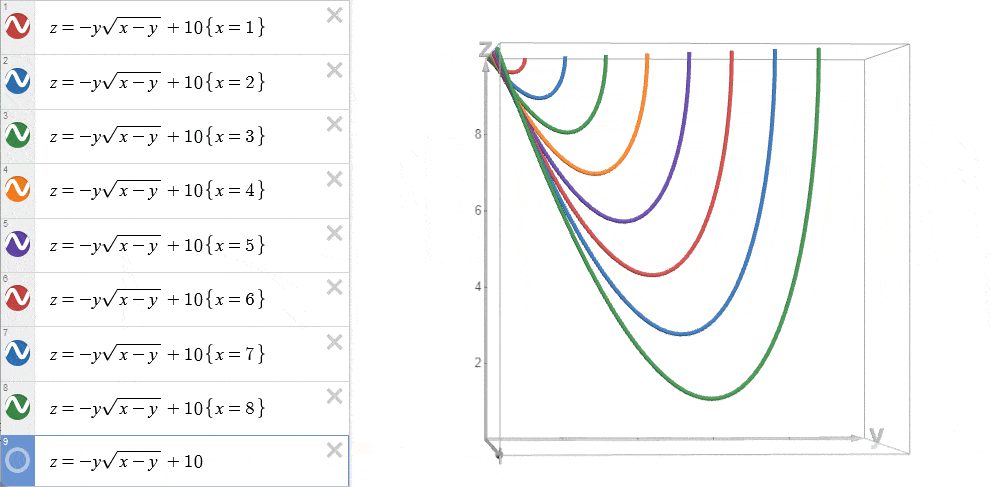
将不同 $x=i$ 的函数 $w(x=i,y=j)$ 绘制在 $w-y$ 平面上。

我们发现，由于 $\frac{\partial^2 w}{\partial x\partial y} \le 0$ ，这些函数的导数随着 $i$ 的增大而递减。

这导致了一个特点：由于这些函数的导数依次减小，所以从起点到最小值点的距离依次增加，最终形成当 $x = i$ 增大时，最小值点对应的 $y=j$ 也随之单调增加。

注

分别从这两个角度出发来解读，结论都是一样的。

只不过题目并不限制 $j$ 的个数，所以一直围绕着 $i$ 来讨论最优策略。如果限制 $j$ 的大小呢？如果有凸性就可以使用WQS二分解除限制。否则分层计算。具体见限制区间个数的情形。

值得关注的地方

四边形不等式并没有限制 $\frac{\partial^2 w}{\partial x^2}$ 和 $\frac{\partial^2 w}{\partial y^2}$ ，所以并不要求是凸函数， $w(x,y=y_0)$ 和 $w(x=x_0,y)$ 也不要求是凸函数。仅仅要求 $w(x,y)$ 满足一部分凸性即可。

最终还需要考虑 $g(j)$ 对于DP计算的影响。

令 $W(i,j)=g(j)+w(i,j)$ ，将其视为关于 $i$ 的一系列只是常数 $j$ 不同的函数的集合。

如果 $g(j)$ 单调不增：

容易想到，每个决策都将有自己的一席之地。（没有 $g(j)$ 时已经就是这样的格局，再加上递减的 $g(j)$ ，局面更加稳固（说的啥🤣））

如果 $g(j)$ 无明显性质：

可能导致有的决策因为 $g(j)$ 变贵了，被其他策略战胜。类似于斜率优化维护凸壳把点弹走的感觉。

反四边形不等式的性质和上面的一切完全相反。注意它求的是最大值。

结论与拓展

对于 $f(i)=\min\limits_{1\le j < i}\{g(j)+w(i,j)\}$ ，需要 $w(i,j)$ 满足四边形不等式：

\[ w(i,j)+w(i+1,j+1)\le w(i,j+1)+w(i+1,j),\quad i<i+1\le j <j+1 \]

速记：左中区间 + 右中区间 $\le$ 大区间 + 小区间

对于 $f(i)=\max\limits_{1\le j < i}\{g(j)+w(i,j)\}$ ，需要 $w(i,j)$ 满足反四边形不等式：

\[ w(i,j)+w(i+1,j+1)\ge w(i,j+1)+w(i+1,j),\quad i<i+1\le j <j+1 \]

速记：左中区间 + 右中区间 $\ge$ 大区间 + 小区间

进行决策单调性优化：设 $k(i)$ 为状态 $i$ 的最优决策点（这里的 $k$ 是 $f(i)$ 取得最优情况的 $j$ ，所以用 $k(i)$ 表示），则有：

\[ \begin{align} k(i-1) \le k(i) \le k(i+1) \end{align} \]

有关四边形不等式的拓展思考

1D/1D 方程

\[ f(i)=\min\limits_{1\le j < i}\{g(j)+w(i,j)\} \]

对于单调队列优化适用的情况： $w(i,j)=a(i)$ 。

易知其满足四边形恒等式：

\[ \frac{\partial^2 w}{\partial x\partial y}=\frac{\partial ^2 w}{\partial y\partial x}=0 \]
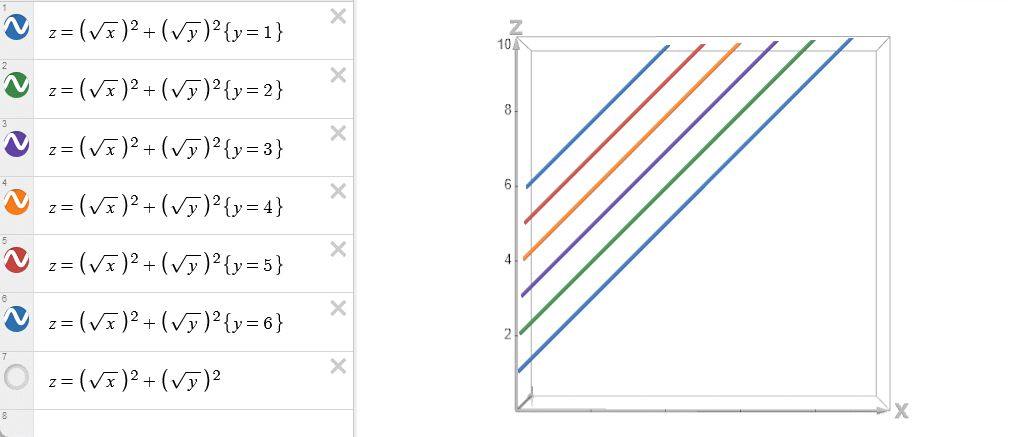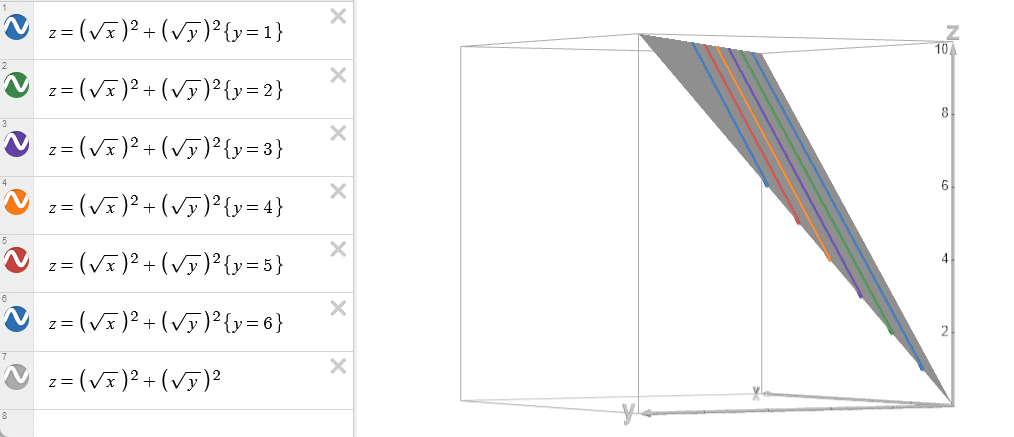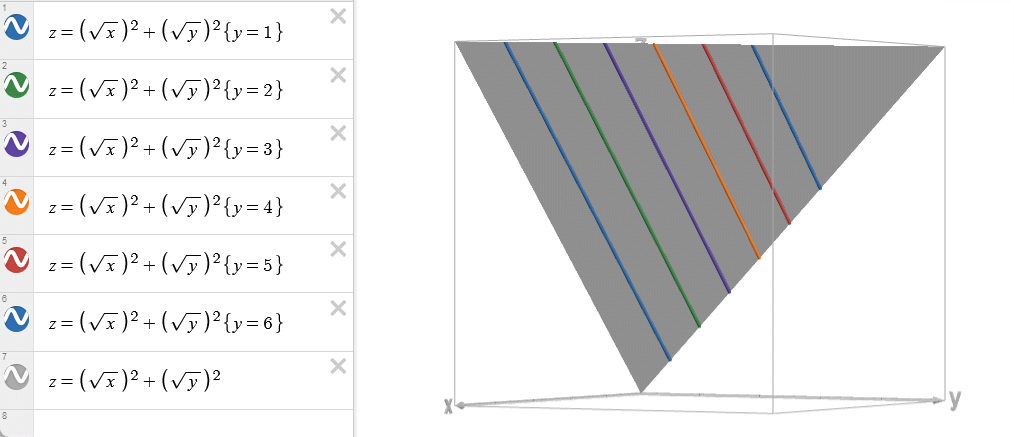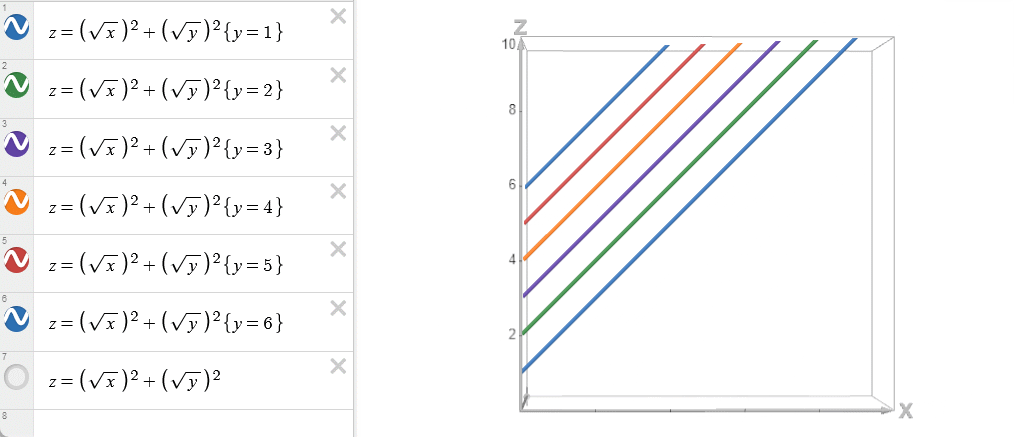
对于斜率优化适用的情况： $w(i,j)=-a(i)d(j)$ 。
1. $a(i)$ 单调，$d(j)$ 单调，且两者单调性相同
  
  \[ \frac{\partial^2 w}{\partial x\partial y}=\frac{\partial^2 w}{\partial y\partial x}=-a'(x)b'(y)\le0 \]
  
  故满足四边形不等式。所以斜率优化实际上是决策单调性的一个特殊情况。
  
  当然还有 $dp(j)$ 的影响，所以一般不是下图如此完美的凸壳，具体见前文“值得关注的地方”

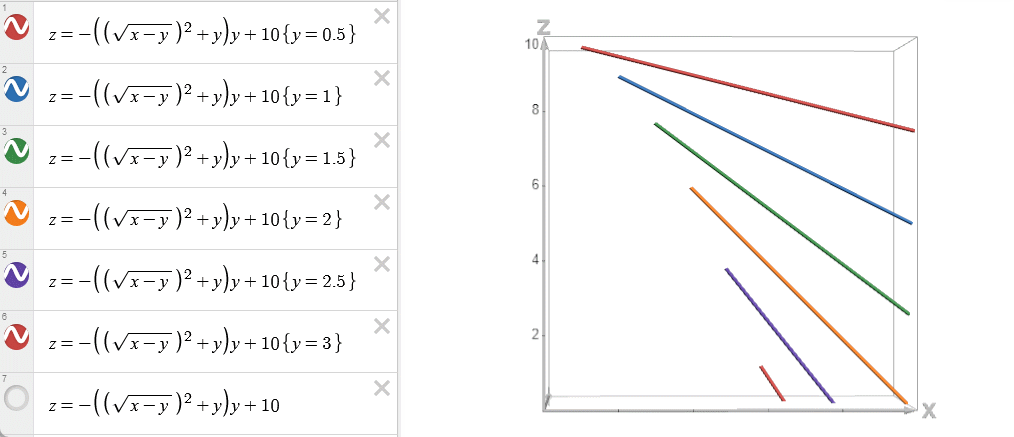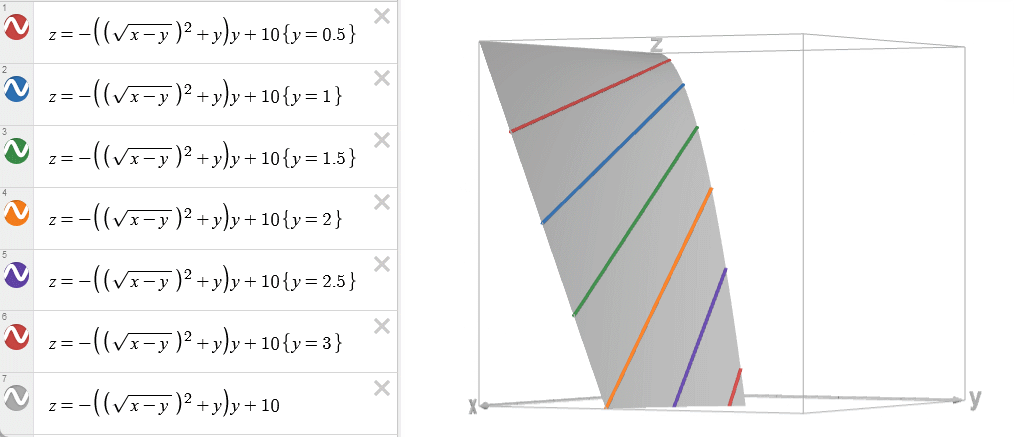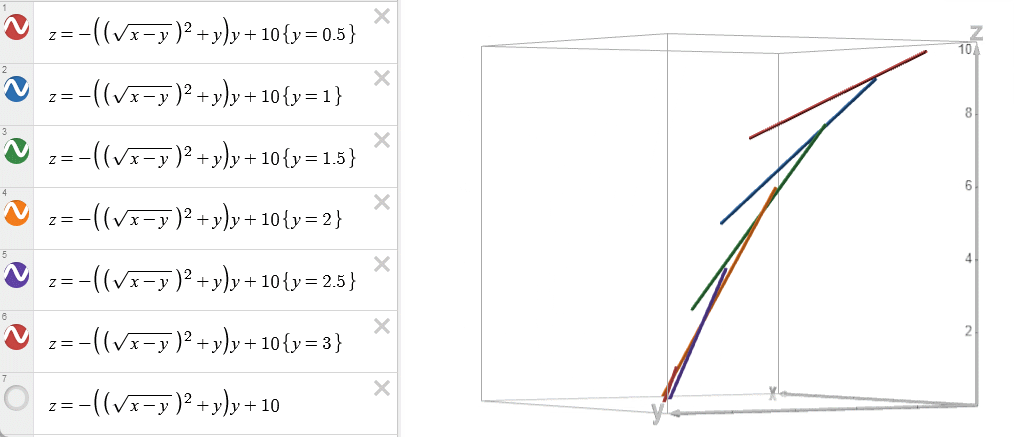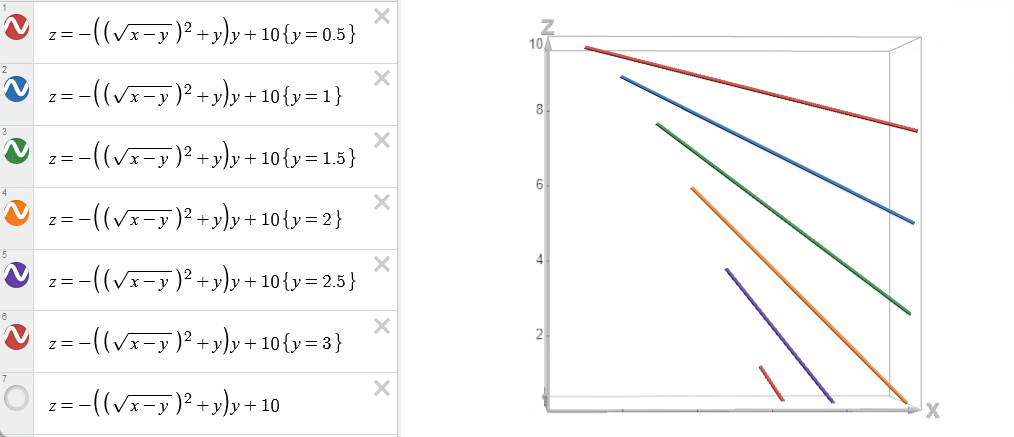
其他情况

此时就没四边形不等式什么事了。我们单纯维护凸壳，每次用 $O(\log n)$ 时间去搜索决策点。这是1D/1D基本上都通用的方法。

(1) 方法一：单调队列 + 二分

若转移方程是 $f_j+w→f_i$，那么求 $f_i$ 前就要先求出前面的所有 $f$，称这个问题为在线问题，无法采用方法二的分治做法。此时可以采用顺序计算的单调队列 + 二分算法。

我们参考斜率优化中用单调队列维护凸壳的策略。不过这里我们构成“凸壳”（不太严谨，或称为最优策略集合）的函数可不是直线了，而是一条条曲线。

可是，为什么标题中又还有“二分”呢？

原来，在斜率优化中，由于 $w(i,j)=-a(i)d(j)$ ，我们可以轻松得知凸壳上的最优决策分界点坐标 $(d(j),f(j))$ ，也就是上图中的 $A,F,D$ 这几个点。然后就可以 $O(1)$ 维护单调队列的队首弹出和队尾压入。

但在这里，我们并不知道 $w(i,j)$ 内部的情况，如何确定两个最优决策之间的分界点呢？

答案很简单：二分。

当我们取出单调队列里保存的两个最优决策 $j_1<j_2$ 时，它们存在一个分界点 $i=t$ 。
在 $[0,t)$ 上，决策 $j_1$ 优于决策 $j_2$ ；在 $(t,N]$ 上，决策 $j_2$ 优于决策 $j_1$ 。
只需要在 $[j_2,N]$ 上二分搜索这个 $t$ 就可以了。因为 $j<i$ ，所以决策 $j_2$ 的最优区间起点一定在 $[i=j_2,N]$ 上

因此，该方法总时间复杂度为 $O(n\log n)$ 。

注意和斜率优化里的二分单调栈区分。它们的二分用途不一样。

建议用一个三元组来描述一个最优策略： $\{i_{left},i_{right},j\}$ 。这样可以避免一点重复计算。不过下面偷懒没搞 XD

代码示例

int dp[MAXN];
int q[MAXN], head, tail;
int G(int j);
int W(int i, int j);
// 计算当x=i，选择决策j时的费用
inline int calc(int i, int j) { return G(j) + W(i, j); }
// 二分找到这两个相邻最优决策的分界点：第一个决策b比决策a优的位置
inline int binSearch(int a, int b) {
    // 决策b全程劣于决策a，返回一个大于N的数值表示无法取得
    if (calc(N, a) < calc(N, b)) return N + 1;
    int l = b, r = N, mid, ans = -1;
    while (l <= r) {
        mid = (l + r) >> 1;
        if (calc(mid, b) > calc(mid, a)) l = mid + 1;
        else r = mid - 1， ans = mid;
    }
    return ans;
}
void solve() {
    dp[0] = 0, q[head = tail = 1] = 0;
    for (int i = 1; i <= N; i++) {
        // 弹出当前最优决策（囊括了i）之前的决策，那些用不上了
        while (head < tail && binSearch(q[head],q[head+1]) <= i) head++;  
        dp[i] = calc(i, q[head]);
        // 计算决策j=i，如果它比队尾的好，就把队尾弹走
        while (head < tail && binSearch(q[tail],i) <= binSearch(q[tail-1],q[tail])) tail--;
        q[++tail] = i;  // 决策j=i存入队尾
    }
}

(2) 方法二：分治法

若转移方程是 $g+w→f$ 的转移，即转移是由一个完全已知的函数或是 DP 数组的上一层得来的，将这种决策单调性视作“离线的”。此时不依赖前面的 $f_{i-1}$ 来计算 $f_i$ ，就可以不顺序计算 $f_i$ 了，能够采用分治的方法，编码更简单。

为了求解所有状态 $1 \leq i \leq n$ 的最优决策点 $j=\mathop{\mathrm{opt}}(i)$，依据决策单调性可采取分治思想。

算法步骤

初始化：首先暴力遍历 $j\in [1,n/2)$ 计算 $\mathop{\mathrm{opt}}(n/2)$，作为分治的中心点。
分治求解：接下来，算法分别计算两个区间 $[1,n/2)$ 和 $(n/2, n]$ 上的 $\mathop{\mathrm{opt}}(i)$。
- 对于前半段 $[1,n/2)$ ，最优决策点 $\mathop{\mathrm{opt}}(i)$ 必然位于 $1$ 和 $\mathop{\mathrm{opt}}(n/2)$ 之间（含端点）。
- 对于后半段 $(n/2, n]$ ，最优决策点 $\mathop{\mathrm{opt}}(i)$ 必然位于 $\mathop{\mathrm{opt}}(n/2)$ 和 $\mathop{\mathrm{opt}}(n)$ 之间（含端点）。
递归处理：对于每个子区间，使用相同的方法进行处理，直至计算出每个问题的最优决策点。

代码示例

// 计算dp[i]选择决策j时的费用
int calc(int i, int j);
// [l,r]是状态i的区间，[k_l,k_r]是决策点j的区间
void dfs(int l, int r, int k_l, int k_r) {
    int mid = (l + r) / 2, k = k_l;
    // 求状态f[mid]的最优决策点（费用最少）
    for (int j = k_l; j <= min(k_r, mid - 1); j++) 
        if (calc(mid, j) < calc(mid, k)) k = j;
    dp[mid] = calc(mid, k);
    // 根据决策单调性得出左右两部分的决策区间，递归处理
    if (l < mid) dfs(l, mid - 1, k_l, k);
    if (r > mid) dfs(mid + 1, r, k, k_r);
}
// ans = dp[n]

算法复杂度分析

时间复杂度：通过记录搜索的上下边界，算法的时间复杂度可以控制在 $O(n\log n)$。
- 递归树的深度为 $O(\log n)$，因为每次问题规模都减半。
- 在每一层递归中，单个决策点最多被计算两次。因此，总的计算次数为 $O(n\log n)$。
空间复杂度：算法的空间复杂度主要由递归栈空间决定，也是 $O(\log n)$。

分治法相比单调队列的优点

若 $w(i,j)$ 不能够 $O(1)$ 计算，但是可以从 $w(i\pm 1,j\pm 1)$ 来 $O(1)$ 递推

此时分治法能够以均摊 $O(1)$ 的速度计算 $w(i,j)$ 。因为 for (int j=kl;j<=min(kr,mid-1);j++) 计算 $w(i,j)$ 的区间是顺序扩大的。

而单调队列在 $[b,N]$ 之间二分，计算 $w(i,j)$ 的区间是乱跳的，不能利用递推优化。

例题：2. [CF868F] Yet Another Minimization Problem

(3) 方法三：SMAWK 算法

有待后续填坑~

https://www.cnblogs.com/p-b-p-b/p/15054179.html

https://www.luogu.com.cn/blog/FunnyCreature/solution-cf1423m

https://www.cnblogs.com/juju527/p/17376826.html

$O(n+m(1+\max(\log \dfrac n m,0)))$

https://github.com/Itst00/APIO2021-monge/tree/main APIO2021-monge 好东西！！！

(4) 方法四：Wilber 算法

有待后续填坑~

https://www.cnblogs.com/p-b-p-b/p/15054179.html

$O(n)$

(5) 方法五：Eppstein 算法

有待后续填坑~

https://www.cnblogs.com/p-b-p-b/p/15054179.html

$O(n)$

决策单调性模板题

1. 【单调队列二分】P1912 NOI2009 诗人小G

题意概述

对一首诗进行排版，诗句长度各异，一行可放下多句，每句用空格隔开。设【不协调度】为每行的实际长度与行标准长度的差值绝对值的P次方之和，要求使得【不协调度】尽量小。句子间用空格隔开，句子顺序不变，不可拆分。

给定诗句数 $N$ 、行标准长度 $L$ 、$P$ 值，输出最小不协调度下的排版，若最小不协调度超过 $10^{18}$ 则输出"Too hard to arrange"。

决策单调性的二分队列解题思路

设 $dp[i]$ 为前 $i$ 个句子的最小不协调度。每句诗的长度为 $a[i]$ ， $sum[i]$ 为前 $i$ 句诗的总长度。则：

\[ dp[i]=\min\limits_{j\in [0,i)}\{dp[j]+|sum[i]-sum[j]+(i-j-1)-L|^P\} \]

意思是将第 $[j+1,i]$ 句作为最后一行，前面的句子最小不协调度为 $dp[j]$ 。这里 $P$ 次数太大不能斜率优化，则尝试证明 $w(i,j)=|sum[i]-sum[j]+(i-j-1)-L|^P$ 满足四边形不等式。

有点不好证，通常可以打表或直接写一下决策单调性看看。

Proof

详细证明

证明：

\[ \begin{align} w(i,j)+w(i+1,j+1) &\le w(i+1,j)+w(i,j+1),~j<i\\ \therefore w(i,j)-w(i+1,j) &\le w(i,j+1)-w(i+1,j+1) \end{align} \]

设 $u=(sum[i]+i)-(sum[j]+j)-(L+1),~v=(sum[i]+i)-(sum[j+1]+j+1)-(L+1)$ ，则：

\[ |v|^P-|v+(a[i+1]|+1)|^P \geq |u|^P -|u+(a[i+1]+1)|^P,~v\le u \]

设 $h(x)=|x|^P-|x+c|^P, c>0$ ，则只需证明它单调递减即可：

\[ \begin{align} &分类讨论:\\ ①&~~x\in [0,+\infty)\\ \therefore&~~h(x)=x^P-(x+c)^P\\ \therefore&~~h'(x)=Px^{P-1}-P(x+c)^{P-1}< 0\\ \\ ②&~~x\in [-c,0) \\ \therefore&~~h(x)=(-x)^P-(x+c)^P\\ \therefore&~~h'(x)=-P(-x)^{P-1}-P(x+c)^{P-1}\\ 若&~P~为奇数：\\ &~~h'(x)=-Px^{P-1}-P(x+c)^{P-1}<0\\ 若&~P~为偶数：\\ &~~h'(x)=Px^{P-1}-P(x+c)^{P-1}<0\\ \\ ③&~~x\in (-\infty,-c)\\ \therefore&~~h(x)=(-x)^P-(-x-c)^P\\ \therefore&~~h'(x)=-P(-x)^{P-1}-P(-x-c)^{P-1}\\ 若&~P~为奇数：\\ &~~h'(x)=-Px^{P-1}-P(x+c)^{P-1}<0\\ 若&~P~为偶数：\\ &~~h'(x)=Px^{P-1}+P(x+c)^{P-1}<0\\ \\ 综&上所述，h'(x)<0。 \end{align} \]

证完后就直接套模板了。单调队列那里和斜率优化的很像，只不过维护的不是斜率，而是决策函数 $w(x,y=j)$ 。维护凸壳时用二分来查找分界点。

#include <bits/stdc++.h>
using namespace std;
#define MAXN 100005
#define MAXL 35
#define EPS 1e-9
typedef long long ll;            // 2^63 - 1 = 9.22e18
typedef unsigned long long ull;  // 2^64 - 1 = 1.84e18
typedef long double ld;          // 1.18e4932
char sen[MAXN][MAXL];
int a[MAXN], sum[MAXN];
int N, L, P;
ld dp[MAXN];
int from[MAXN], cnt[MAXN], stk[MAXN], stkTop;
int q[MAXN], head, tail;
inline ld fastPow(ld bottom, int hat) {
    ld res = 1.0l;
    while (hat) {
        if (hat & 1) res *= bottom;
        bottom *= bottom;
        hat >>= 1;
    }
    return res;
}
// 计算当x=i，选择决策j时的费用
inline ld calc(int i, int j) {
    int w = abs(sum[i] - sum[j] + i - j - 1 - L);
    return dp[j] + fastPow(w, P);
}
// 二分找到这两个相邻最优决策的分界点：第一个决策b比决策a优的位置
inline int binSearch(int a, int b) {
    // 决策b全程劣于决策a，返回一个大于N的数值表示无法取得
    if (calc(N, a) < calc(N, b)) return N + 1;
    int l = b, r = N, mid, ans = -1;
    while (l <= r) {
        mid = (l + r) >> 1;
        if (calc(mid, b) > calc(mid, a)) l = mid + 1;
        else r = mid - 1， ans = mid;
    }
    return ans;
}
void solve() {
    fill(dp, dp + N + 1, LDBL_MAX);
    dp[0] = 0, q[head = tail = 1] = 0;
    for (int i = 1; i <= N; i++) {
        // 弹出当前最优决策（囊括了i）之前的决策，那些用不上了
        while (head < tail && binSearch(q[head],q[head+1]) <= i) head++;  
        dp[i] = calc(i, q[head]);
        from[i] = q[head];  // 记录从哪里转移过来，用于输出结果
        cnt[i] = i - q[head];
        // 计算决策j=i，如果它比队尾的好，就把队尾弹走
        while (head < tail && binSearch(q[tail],i) <= binSearch(q[tail-1],q[tail])) tail--;
        q[++tail] = i;  // 决策j=i存入队尾
    }
    if (dp[N] > 1e18l) {
        cout << "Too hard to arrange\n--------------------\n";
        return;
    }
    cout << (ull)dp[N] << endl;
    stkTop = 0;
    for (int i = N; i; i = from[i]) stk[++stkTop] = i;
    for (int i = stk[stkTop--], rp = 1;;) {
        for (int j = rp; j < rp + cnt[i]; j++) {
            cout << sen[j];
            if (j < rp + cnt[i] - 1) cout << " ";
            else cout << '\n';
        }
        rp += cnt[i];
        if (stkTop) i = stk[stkTop--];
        else break;
    }
    cout << "--------------------\n";
}
int main() {
    ios::sync_with_stdio(false); cin.tie(0);
    int t; cin >> t;
    while (t--) {
        cin >> N >> L >> P;
        for (int i = 1; i <= N; i++) {
            cin >> sen[i];
            a[i] = strlen(sen[i]);
            sum[i] = sum[i - 1] + a[i];
        }
        solve();
    }
    return 0;
}

2. 【分治法】CF868F Yet Another Minimization Problem

题意概述

给定一个序列 a，要把它分成 k 个子段。每个子段的费用是其中相同元素的对数。求所有子段的费用之和的最小值。

单调决策性的分治法解题思路

确定状态转移方程

设 $dp[i][k]$ 为前 $i$ 个数分成 $k$ 个子段的最小费用之和。则：

\[ dp[i][k] = min(dp[j][k-1] + cost(j+1, i)) \]

其中 $cost(j+1, i)$ 为区间 $[j+1,i]$ 的费用。 $dp[j][k-1]$ 可以看作 $g(j)$ ， $cost(j+1, i)$ 可以看作 $w(i,j)$ 。
证明 $w(i,j)$ 满足四边形不等式

即证明 $w(i,j) + w(i+1,j+1) \le w(i+1,j) + w(i,j+1)$ 。考虑 $a[i]$ 和 $a[j]$ 的情况：
- 若 $a[i]=a[j]$ 且区间 $[j+1,i]$ 内有和它们相等的数，则 $w(i+1,j) + w(i,j+1)$ 会比 $w(i,j)+w(i+1,j+1)$ 多了一个 $a[i]$ 和 $a[j]$ 的对数。
- 其他情况，等式成立。
因此， $w(i,j)$ 满足四边形不等式。
决策单调性实现算法

由于 $w(i,j)$ 并不是 $O(1)$ 计算的，所以用单调队列就比较慢了。但是注意到 $w(i,j)$ 可以由 $w(i+1,j)$ 和 $w(i,j+1)$ 递推得到。因此采用分治法。
区间 $[j+1,i]$ 的费用计算

参考离线莫队里面用左右两个指针表示当前计算的区间值，并暴力移动来维护区间的费用。因为我们是分治法，所以在计算mid的最优决策时左右指针依次移动一步即可，是 $O(1)$ 的。这就是分治法的优势。
注意要开 long long

时间复杂度大概是 $O(kn\log n)$ 。这里的受限制参数 $k$ 比较小，虽然有凸性但WQS二分区间太大，反而不如直接遍历来得快。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define MAXN 100005
int N, K, a[MAXN], cnt[MAXN], wl = 1, wr;
ll dp[MAXN][2], now = 0, pre = 1, w;
inline ll cost(int l, int r) {
    while (wl > l) wl--, w += cnt[a[wl]]++;
    while (wr < r) wr++, w += cnt[a[wr]]++;
    while (wl < l) w -= --cnt[a[wl]], wl++;
    while (wr > r) w -= --cnt[a[wr]], wr--;
    return w;
}
inline ll calc(int i, int j) {
    return dp[j][pre] + cost(j+1, i);
}
void divide(int l, int r, int kl, int kr) {
    int mid = (l + r) >> 1, k = kl;
    ll kval = calc(mid, k);
    for (int j = kl; j <= min(kr, mid); j++) {
        ll tmp = calc(mid, j);
        if (tmp < kval) k = j, kval = tmp;
    }
    dp[mid][now] = kval;
    if (l < mid) divide(l, mid - 1, kl, k);
    if (r > mid) divide(mid + 1, r, k, kr);
}
int main() {
    ios::sync_with_stdio(false); cout.tie(0); cin.tie(0);
    cin >> N >> K;
    wr = N;
    for (int i = 1; i <= N; i++) {
        cin >> a[i];
        dp[i][now] = (w += cnt[a[i]]++);
    }
    for (int i = 2; i <= K; i++) {
        swap(now, pre);
        divide(1, N, 1, N);
    }
    cout << dp[N][now];
    return 0;
}

3. 【分治法】POI2011 Lightning Conductor

题目大意

给定一个长度为 $n$ 的序列 $\{a_n\}$，对于每个 $i\in [1,n]$ ，求出一个最小的非负整数 $p$ ，使得 $\forall j\in[1,n]$，都有 $a_j\le a_i+p-\sqrt{|i-j|}$

$1 \le n \le 5\times 10^{5}$，$0 \le a_i \le 10^{9}$ 。

单调决策性的二分队列解题思路

设 $dp[i]$ 为第 $i$ 个数的最小 $p$ 值（注意不是 $\min$ ，我们要看 $p$ 的式子，那个计算是 $\max$ 计算）。则：

\[ \begin{align} p_i &= \max\limits_{j\in [0,i)}\{a_j-a_i+\sqrt{|i-j|}\}\\ p_i &= \max\limits_{j\in [0,i)}\{a_j+\sqrt{|i-j|}-a_i\}\\ \text{Let } w(i,j) &= \sqrt{|i-j|}-a_i,~g_j=a_j\\ \therefore f_i &= \max\limits_{j\in [0,i)}\{g_j+w(i,j)\} \end{align} \]

小证一下 $w(i,j)$ 满足四边形不等式：

\[ \begin{align} \text{TBD: }&~w(i,j)+w(i+1,j+1) \le w(i+1,j)+w(i,j+1)\\ \text{Namely: }&~\sqrt{|i-j|}+\sqrt{|i+1-j-1|} \le \sqrt{|i+1-j|}+\sqrt{|i-j+1|}\\ \text{That is: }&~2\sqrt{|i-j|} \le 2\sqrt{|i-j+1|}\\ \end{align} \]

显然成立。直接用分治法套模板即可。

注意这里由于绝对值的存在， $j$ 是会大于 $i$ 的。可以看作两个不同的问题。我们将序列反转，做第二遍分治，取两次分治的最大值即可。

#include <bits/stdc++.h>
using namespace std;
int n, a[500005];
double p[500005];
#define calc(i, j) (a[j] + sqrt(abs(i - j)) - a[i])
void divide(int l, int r, int kl, int kr) {
    int mid = (l + r) >> 1, k = kl;
    double kval = calc(mid, kl), tmp;
    for (int j = kl; j <= min(kr, mid); j++) {// 这里j=mid可以，此时为tmp=0被排除，也可以改为mid-1
        tmp = calc(mid, j);
        if (tmp > kval) k = j, kval = tmp; // 取最大的p
    }   
    p[mid] = max(p[mid], kval);    // 两次，取最大的
    if (l < mid) divide(l, mid - 1, kl, k);
    if (mid < r) divide(mid + 1, r, k, kr);
}
int main() {
    ios::sync_with_stdio(false); cout.tie(0); cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    divide(1, n, 1, n);
    reverse(a + 1, a + n + 1); // 由于只处理了 j <= i 的决策，还要倒过来在算一遍
    reverse(p + 1, p + n + 1);
    divide(1, n, 1, n);
    for (int i = n; i >= 1; i--) cout << (int)ceil(p[i]) << '\n'; // 小数向上取整
    return 0;
}

决策单调性练习题

单调队列二分

P1973 NOI2011 Noi嘉年华

P3724 [AHOI2017/HNOI2017] 大佬

分治

P5504 [JSOI2011] 柠檬

4 (2D/1D) 四边形不等式优化

概念

这里的四边形不等式优化指的是区间决策单调性优化。

四边形不等式常用于优化 2D/1D 方程，意思是我们计算的 $dp[i][j]$ 的状态维度是 2 维的 $[i][j]$ ，决策点的维度是 1 维的 $[k]$ 。

四边形不等式特征状态方程：

\[ \begin{align} dp[i][j] &= \min\{dp[i][k]+dp[k+1][j]+w[i][j]\},\quad k \in [i,j-1] \\ &=\min\{dp[i][k]+dp[k+1][j]\}+w[i][j] \end{align} \]

四边形不等式：

\[ \begin{align} w(a,c)+w(b,d)&\le w(a,d) + w(b,c),\quad a\le b\le c\le d\\ 或者~w(i,j)+w(i+1,j+1)&\le w(i,j+1) + w(i+1,j),\quad i<i+1\le j <j+1 \end{align} \]

速记：左中区间 + 右中区间 $\le$ 大区间 + 小区间

单调性：

\[ 对任意~a\le b\le c\le d,~有~w(b,c) \le w(a,d). \\ 或者~w(i+1,j) \le w(i,j+1) \]

速记：小区间 $\le$ 大区间，类似于一维的单调递增

四边形不等式定理：如果 $w(i,j)$ 满足四边形不等式和单调性，则用DP计算 $dp[][]$ 的时间复杂度为 $O(n^2)$

引理 1：如果 $w(i,j)$ 满足四边形不等式和单调性，则 $dp[i][j] = \min(dp[i][k]+dp[k+1][j]+w[i][j])$ 也满足四边形不等式。

引理 2：记 $s[i][j]=k$ 为 $dp[i][j]$ 取得最小值时的 $k$，如果 $dp[i][j]$ 满足四边形不等式，则有：

\[ s[i][j-1]\le k \le s[i+1][j] \]

速记：左中区间 $\le$ 大区间 $\le$ 右中区间

反四边形不等式特征状态方程（min变为max）：

\[ \begin{align} dp[i][j] &= \max\{dp[i][k]+dp[k+1][j]+w[i][j]\},\quad k \in [i,j-1] \\ &=\max\{dp[i][k]+dp[k+1][j]\}+w[i][j] \end{align} \]

反四边形不等式（$\le$ 变为 $\ge$）：

\[ \begin{align} w(a,c)+w(b,d)&\ge w(a,d) + w(b,c),\quad a\le b\le c\le d\\ 或者~w(i,j)+w(i+1,j+1)&\ge w(i,j+1) + w(i+1,j),\quad i<i+1\le j <j+1 \end{align} \]

速记：左中区间+右中区间 $\ge$ 大区间+小区间

单调性（$\le$ 变为 $\ge$）：

\[ 对任意~a\le b\le c\le d,~有~w(b,c) \ge w(a,d). \]

速记：小区间 $\ge$ 大区间，类似于一维的单调递减

反四边形不等式定理：如果 $w(i,j)$ 满足反四边形不等式和单调性，则用DP计算 $dp[][]$ 的时间复杂度为 $O(n^2)$

引理 3：如果 $w(i,j)$ 满足反四边形不等式和单调性，则 $dp[i][j] = \max(dp[i][k]+dp[k+1][j]+w[i][j])$ 也满足反四边形不等式。

引理 4：记 $s[i][j]=k$ 为 $dp[i][j]$ 取得最大值时的 $k$，如果 $dp[i][j]$ 满足反四边形不等式，则有（和前面的相同）：

\[ s[i][j-1]\le k \le s[i+1][j] \]

速记：左中区间 $\le$ 大区间 $\le$ 右中区间

区间决策单调性模板题

石子合并问题

$\texttt{Description}$

有 n 堆石子排成一排，每堆石子有一定的数量。每次可以将两堆相邻的石子堆合并，合并后的石子堆的数量为两堆石子堆的数量之和。合并的费用为两堆石子堆的数量之和。经过n-1次合并后，所有的石子堆都被合并成了一堆，求出总费用的最小值。

$\texttt{Input}$

第一行：n，表示石子堆数目；第二行：n个数，表示每堆石子的数量

$\texttt{Output}$

输出总费用的最小值 (附加：求最大值)

$\texttt{Hint}$

合并过程：(2,4,5) -> (6,5) -> (11) 总费用为17

题解

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
const int N = 1002;
int n;
int w[N];      // 前缀和维护[i,j]中的所有石子数量
int dp[N][N];  // dp[i][j] 表示合并[i,j]中石子的最优值
int s[N][N];   // s[i][j] 表示最佳分割点
#define sum(i, j) w[j] - w[i - 1]
int main() {
    cin >> n;
    for (int i = 1, tmp; i <= n; i++) {
        cin >> tmp;
        w[i] = w[i - 1] + tmp;
    }

    // 求最小值
    memset(dp, INF, sizeof(dp));
    for (int i = 1; i <= n; i++) {
        dp[i][i] = 0;
        s[i][i] = i;
    }
    for (int len = 2; len <= n; len++) {
        for (int i = 1, j = i + len - 1; j <= n; i++, j++) {
            // 此处用四边形不等式优化，因为sum[i,j]满足四边形恒等式和单调递增（单调递增只是比喻的说法）
            // 原本的 for (int k = i; k < j; k++) 优化为下面的
            // 注意右侧区间端点是 <=
            for (int k = s[i][j - 1]; k <= s[i + 1][j]; k++) {
                if (dp[i][j] > dp[i][k] + dp[k + 1][j] + sum(i, j)) {
                    dp[i][j] = dp[i][k] + dp[k + 1][j] + sum(i, j);
                    s[i][j] = k;
                }
            }
        }
    }
    cout << dp[1][n] << endl;

    // 下面求最大值，这个要改一下初始化
    memset(dp, 0, sizeof(dp));
    for (int i = 1; i <= n; i++)
        dp[i][i] = 0;
    for (int len = 2; len <= n; len++) {
        for (int i = 1, j = i + len - 1; j <= n; i++, j++) {
            // 此处不可以用反四边形不等式优化，因为sum[i,j]不满足单调递减（单调递减只是比喻的说法）
            for (int k = i; k < j; k++) {
                dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + sum(i, j));
            }
        }
    }
    cout << dp[1][n] << endl;

    return 0;
}

5 (2D/1D) WQS带权二分优化

特征状态方程：

\[ \begin{align} &f(i,j)=\min/\max\{g(i,k)+w(i,j)\},\quad j \in [1,i],\quad w(i,j)~无明显性质 \\\\ &令~i~为常数，f(j)~为凸函数，即~f(j)-f(j-1)\le f(j+1)-f(j)~或~f(j)-f(j-1)\ge f(j+1)-f(j)~\\\\ &令~j \to +\infty，f(i)=\min/\max\{g(i)+w(i,j)\} ~能在~O(n)~时间内计算。 \end{align} \]

题目类型

给定 $N$ 个物品，每个物品有其价值 $w$（$w$ 可以为负数），限制从其中选取 $M$ （$m \le n$）个物品，求最大选取总价值。

朴素DP思路

（这里看似可以直接排序 $O(n\log n)$ ，但是题目中价值 $w$ 往往较复杂，不能简单的排序后贪心）

设 $f(i,j)$ 为前 $i$ 个物品中，选取 $j$ 个物品的最大价值。则状态转移方程为：

\[ f(i,j)=\max\{f(i-1,j),f(i,j-1)+w(i)\},\quad j \in [1,i] \]

这个朴素版本的做法的时间复杂度是 $O(n^2)$ 。而WQS二分能优化至 $O(n\log n)$ 。

WQS二分解题思路

1. 检查 $f(i=C,j)$ 关于 $j$ 的凸性

既然要优化，那么一定是利用了函数的某种性质，这里也是利用的凹凸性。

将 $f(i,j)$ 看作以选取物品 $j$ 为自变量的函数，$i$ 为其中的常数，把 $j$ 改写为 $x$ ，则有函数 $f(i=C,x)$ 。

注意到 $f(i=C,x)$ 为上凸函数，即满足：

\[ f(x-1)-f(x) \ge f(x) - f(x+1) \]

这个很容易想到，我们每次选取物品，必然选最好的，下一轮选择肯定只能选到没那么好的或同样好的。这增长率不就单调不减了嘛。

2. 简化问题：不限制 $j$ 时的 $f(i,j=不限制)$ 很好算

假设不限制选取物品个数，求最大选取总价值。当然全都选就是 $N$ 个。则：

\[ f(i,x=不限制)=\max\{f(i-1),f(i-1)+w(i)\}, \quad i \in [1,N] \]

这个是一个 $O(n)$ 的过程。最终答案为 $f(i=N)$ 。

此时选取了 $0\le t \le N$ 个物品。虽然没有指定一定要选几个，但只选 $t$ 个是最优的，剩下的物品是负数，不选。所以 $f(i=N,x=t)=f(i=N)$ 。这样就以 $O(n)$ 时间就算出了 $f(N,t)$ 。

要是 $t=M$ 的话，岂不是直接算出了 $f(N,M)$ ！？确实如此，但可惜 $f(i=C,x)$ 的最大值点不一定是 $M$ 。

3. 凸函数：加减 $kx$ 凸性不变，最值点单调移动

现在我们来观察凸函数的性质：（以二次函数为例）

“用原凸函数构造新凸函数，用新凸函数的最值点，可以反求原凸函数上横坐标相同的点。”

“而凸函数的最值点很好计算，进而加速了原凸函数上任意一点的计算。”

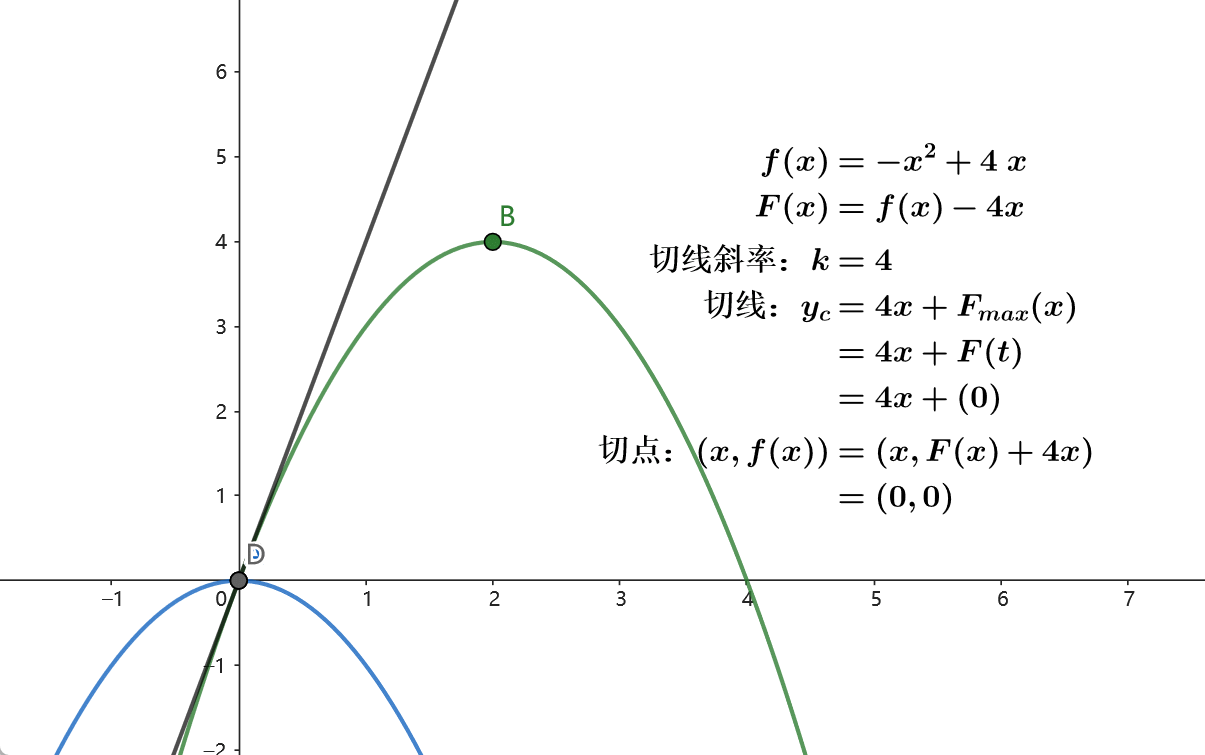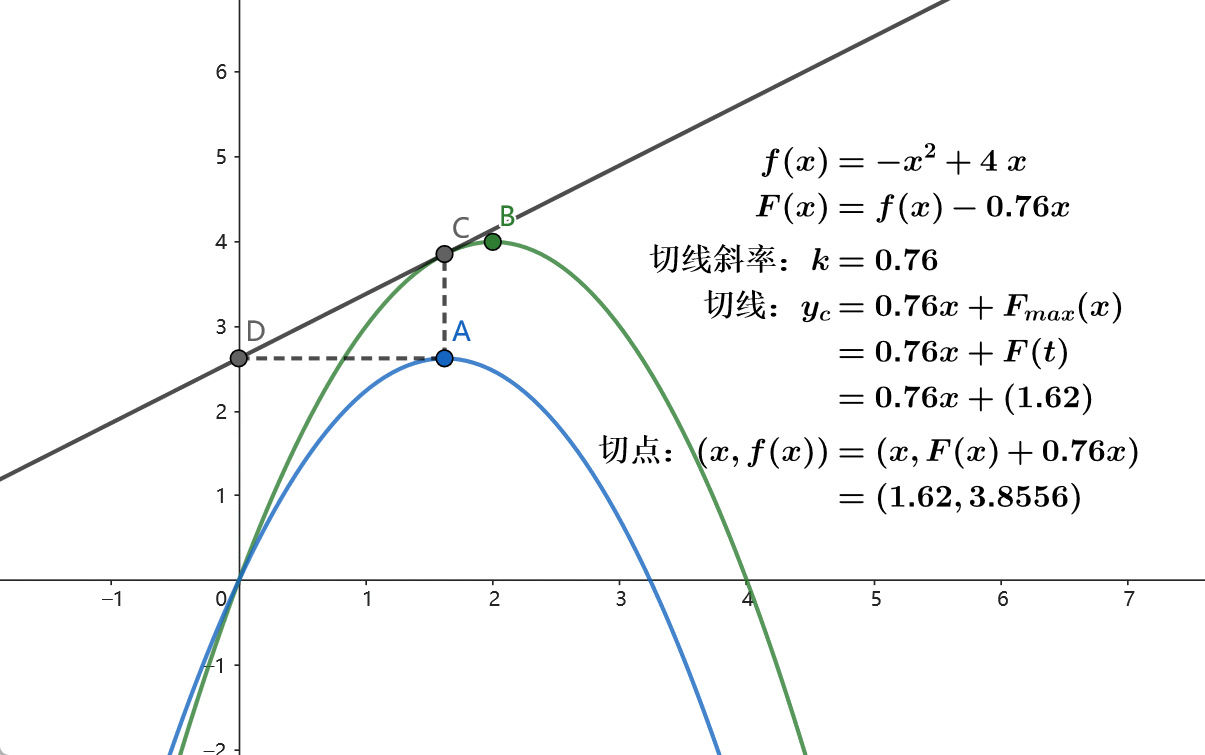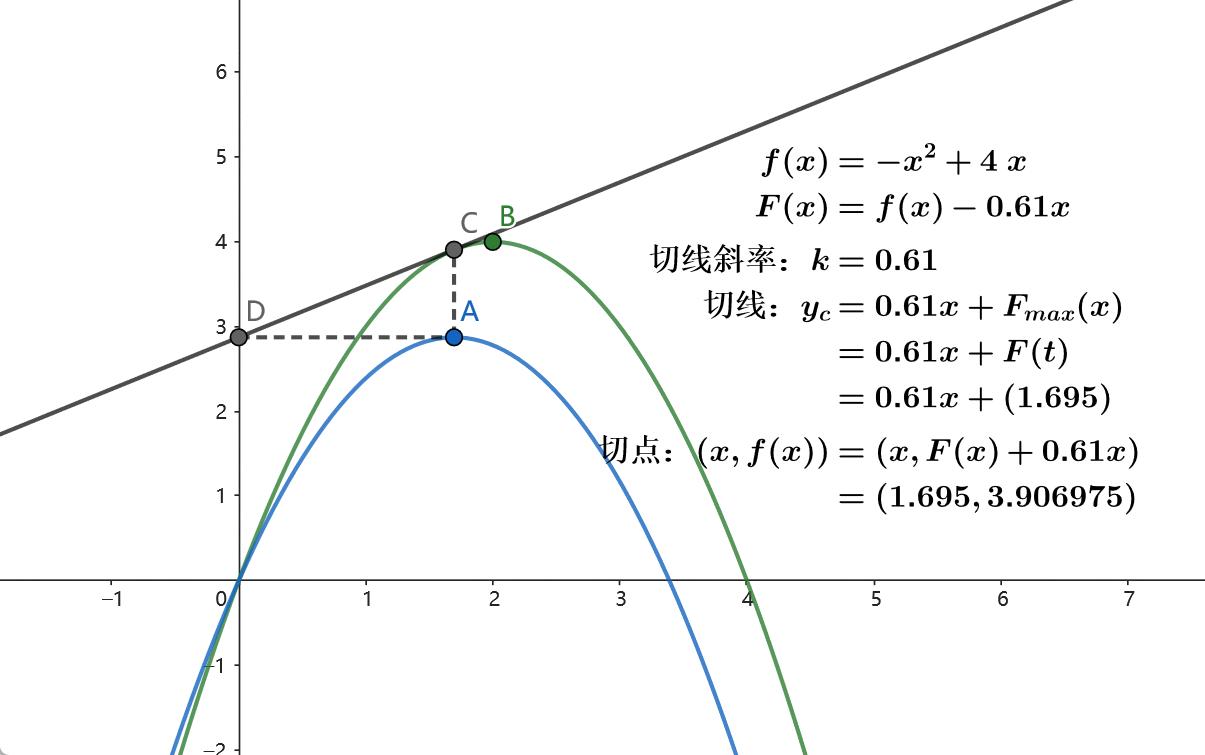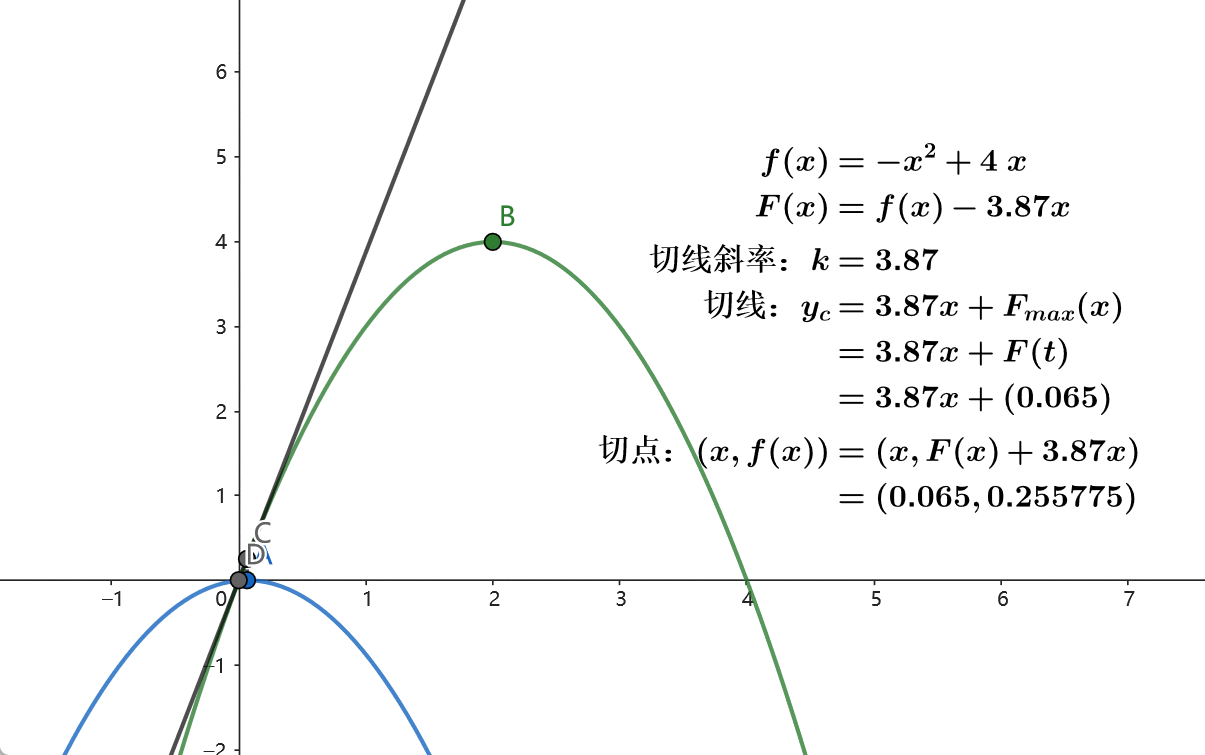
在二次函数 $y=ax^2+bx+c$ 中，最值点的横坐标为 $t=-\frac{b}{2a}$ 。给函数减去 $kx$ 相当于减小 $b$ 的值，此时最值点的横坐标增大。所以 $F(x)=f(x)-kx$ 的最值点横坐标 $t'$ 关于 $k$ 是单调的。

当我们遍历所有的 $k$ 值，就可通过不同的 $F_{max}(x)=F(t)$ 计算出 $f(x)$ 上的所有点。我们通过二分搜索来查找 $F_{max}(x)=F(t=M)$ 对应的 $k$ 值，即可得到 $f(x=M)$ 。如果这里常量 $i=N$ ，则得到了 $f(N,M)$ 。

实际上，所有与 $f(x)$ 相交的直线 $y=kx+F(x)$ 构成了 $F(x)$ 的图像。所以当 $y=kx+F(x)$ 是 $f(x)$ 的切线时，取得 $F(x)$ 的最值点。

4. 加减 $kx$ 构造新凸函数，用其最值点求 $f(i,j)$

前面是连续函数，下面我们来看离散型的函数是否也是这样。

我们利用其凸性，用一条直线对其相切：

\[ f(j) = kj + b \]

为了更加直观，写为 $f(x)=kx+b$ 。我们设 $F(x)=b=f(x)-kx$ 。这里设常数 $i=N$。

图中 $f(N,x)$ 上的每个点都需要 $O(n^2)$ 的时间计算得出。如果我们计算 $f(N,x=不限制)$ ，就是 $O(n)$ 。

是否有办法让 $f(N,x)$ 上任意一点的计算速度和 $f(N,x=不限制)$ 一样快？

我们发现可以利用切点来计算 $f(N,x)$ 。令 $f(N,x)=kx+b$ ，截距 $b=f(N,x)-kx=F(N,x)$ 。

假设 $x=t$ 时取得 $F(N,x)$ 的最大值，此时 $b_{max}=F_{max}(N,x)=F(N,t)$ 就是 $f(N,x)$ 的切线的截距。根据计算得出的切线 $y=kx+b_{max}$ ，我们就可以计算得到 $f(t)=kt+b_{max}$ 。

现在我们思考 $F(N,x=不限制)$ 的情况：

我们计算 $F(N,x=不限制)$ 的最优值，那么它自然一定是 $F(N,x)$ 的最大值。并且通过证明可知 $t \in [1,N]$ 。简单的高中方法证明如下：

\[ \begin{align} 设&~f(x)~为前~N~个物品中取~x~个物品时的最大总价值。这里不再把~N~写在函数参数括号中。\\ \because&~~~f(x)-f(x-1)\ge f(x+1)-f(x)。\\ \therefore&~~f(x)~为上凸函数，f''(x)\le 0。\\ 设&~F(x)=f(x)-kx,~~F_{max}(x)=F(t)。 \\则&~F'(x)=f'(x)-k，F''(x)=f''(x)\le 0，F(x)~也为上凸函数。\\ \\ 对&~f'(x)~进行分类讨论:\\ ①&~~f'(1)\lt k,~~f'(N)\gt k \\ &~~由于~f'(x)~单调不增，不成立，舍去。\\ \\ ②&~~f'(1)\lt k,~~f'(N)\le k \\ &~~由于~f'(x)~单调不增，故~f'(x)<k。\\ \therefore&~~~F'(x)< 0,~F(x)~单调递减。\\ \therefore&~~~F(t)=F_{max}(x)=F(1)\\ \\ ③&~~f'(1)\ge k,~~f'(N)\gt k \\ &~~~由于~f'(x)~单调不增，故~f'(x)>k\\ \therefore&~~~F'(x)>0,~F(x)~单调递增。\\ \therefore&~~~F(t)=F_{max}(x)=F(N)\\ \\ ④&~~f'(1)\ge k,~~f'(N)\le k \\ \therefore&~~~F'(1)=f'(1)-k \ge 0,~~F'(N)=f'(N)-k \le 0\\ \therefore&~~~ 由零点定理可得~F(x)~极大值点~t \in[1,N]。\\ \\ 综&上所述，F(x)的极大值点~t \in[1,N]。 \end{align} \]

所以：

\[ \begin{align} F_{max}(N,x)&=F(N,t)=F(N,x=不限制),\quad t \in [1,N] \end{align} \]

我们算出了该 $k$ 值下的 $F_{max}(N,x)$ 之后，此时 $b_{max}=F_{max}(N,x)$ 就是 $f(N,x)$ 的切线的截距。根据切线 $y=kx+b_{max}$ ，就可以得到 $f(N,t)$ 上的切点 $(t,kt+b_{max})$ ，也就计算出了 $f(N,t)$ ：

\[ f(N,t)=kt+b_{max}=kt+F(N,t)=kt+F(N,x=不限制) \]

其中 $F(N,x=不限制)$ 的计算是 $O(n)$ 的：（下面 $i$ 意思是前 $i$ 个物品中取不限制个物品）

\[ F(i)=max\{F(i-1),F(i-1)+w(i)-k\},\quad i \in [1,N] \]

5. 二分搜索合适的 $k$ 值，得到 $f(N,M)$

这是不是意味着计算 $f(N,x)$ 的速度变成了 $O(n)$ 呢？还不是。因为我们并不能控制 $t=M$ ，所以我们该如何得到想要的 $f(N,M)$ 呢？难道碰运气？

观察 $k$ 取不同值时的 $F(N,x)$ 图像，容易发现它的极值点 $x=t$ 随 $k$ 的增大而减小，这是由于 $f(N,x)$ 的凸性导致的。这个也很好证明，但是懒得写了。ψ(｀∇´)ψ

因此，我们可以考虑在一定范围内对 $k$ 进行二分搜索，直到找到某个 $F_k(N,x)$ 的极大值点 $x=t=M$ ，这样我们就获得了 $f(N,M)$ 的值。二分搜索的时间复杂度为 $O(\log n)$ ，每次计算 $F_k(N,x=不限制)$ 的时间复杂度为 $O(n)$ ，总时间复杂度为 $O(n\log n)$ 。

还可以对WQS二分这样简单理解：每选取一个物品，额外减少 k 的价值，从而间接限制DP对物品的选择数量。

对 $k$ 进行二分搜索的范围，最大为 $[0,\max\{w(i)\}]$ 。

由于本题 $f(x)$ 的斜率 $f'(N,x)=f(N,x)-f(N,x-1)$ 始终为整数，所以切点 $(t,kt+b_{max})\in f(N,x)$ 的 $k$ 也为整数，因此只需要整数二分。如果斜率存在小数，则需要实数二分，涉及到浮点数中的精度处理。可以固定实数二分的查找次数，以决定 $k$ 的精度。

6. 特别注意事项

(1) 注意多点共线

需要特别特别注意的是你的 整数二分和 $F_k(N,x=不限制)$ 的计算要匹配！！！

如果 F 的最值是多点共线，我们将不能简单地通过整数二分搜索直接获得中间的点，只能获得端点。搜索出的 $x=t$ 并不一定等于 $M$ ！！！但是可以由端点计算中间的点，因为它们的 $F$ 的值都是一样的，只是 $f$ 需要加上的 $kx$ 不同。

当我们计算出共线的某一个端点的 $F_{max}(N,x)$ 时，则可以计算出这条线段上的所有 $f(N,x)$ 的值，具体见模板题。

如果一不注意就会 WA ！！！！！！！！！！！！QwQ

当然实数二分就基本上没有这个烦恼，但是要注意处理好 eps 。

例题：WQS二分模板题第1题：邮局；WQS二分练习题：aliens

(2) 注意 M 是否永远无法通过二分取到

如果 $t < M _orM<t $ 成立，则 $M$ 对应的 $F(N,M)$ 100%和二分边界的 $F(N,t)$ 共线，如果你的 $f(N,M)$ 计算放在二分循环内，将要特别考虑此种情况。

具体见练习题：P1484 种树的这行代码：if (ans == -1) ans = val + k * mid;

ll l = 0, r = *max_element(a + 1, a + n + 1), mid, val, cnt, ans = -1;
while (l <= r) {
    mid = l + ((r - l) >> 1);
    tie(val, cnt) = check(mid, ans);
    if (cnt >= k) l = mid + 1, ans = val + k * mid;
    else r = mid - 1;
}
// 因为 cnt 最大为树坑为非负数的个数，所以 cnt 可能恒小于 k
if (ans == -1) ans = val + k * mid;

WQS二分的拓展

A. 多重WQS二分

如果同时对两个受限制的变量进行二分，则相当于在凸曲面上寻找最值，利用的是曲面的凸性。

可以拓展至对任意多个受限制的变量进行二分，只要你能证明关于每个变量的 $f$ 都有凸性。

我们首先将问题简化为每一个变量都不受限制的情况，得到此时的 $f(i)$ ，然后设计 $F(x)$ 。通过多层嵌套的二分搜索（每一层搜索一个变量的 $k$ 值）搜索结果。

例题：WQS二分模板题第2题：CF739E Gosha is hunting

B. 对任意凸函数中受限制变量进行二分

是的，WQS二分不仅仅可用于一般的DP最优化问题。只要你的问题是最优化问题，含有受限制参数，函数关于受限制变量是凸函数，就可以二分这个额外权重 $k$ 来搜索答案。（和树、图等等结合）

例题：WQS二分模板题第3题：P2619 [国家集训队] Tree I

C. 对非凸函数进行WQS二分

以下内容仅仅为个人猜想，正确性未经过证明。

Conjecture

对非凸函数使用WQS二分的猜想

设状态转移方程为： $f(i,j)=optim\{g(i,j)+w(i)\}=optim\{G(i,j)\}$ 。

则我们观察函数性质的域为： $\begin{align}f(N,j)&=optim\{g(N,j)+w(N)\}=optim\{G(N,j)\}\\ \Rightarrow f(x)&=optim\{G(x)\}\end{align}$ 。

如果当 $f(i,j)$ 关于 $j$ 不是凸函数，但定义域内只有一个极值点，即 $f'=0$ 在定义域内有且仅有一个解，此时也是可以通过某种手段构造出极值点偏移的新函数的。但是就不是 $kx$ 了，可能是 $k\ln x$ 、$k\sqrt{x}$ 、$\frac{k}{x}$ 等等。具体如何选择合适的偏移项来构造，需要具体观察。

例一

下式中 $f$ 并不是凸函数，因为 $f''=\frac{2\ln x-3}{x^3}$ 有一个零点。我们参考 $f$ 构造新的函数 $F$ ，并且使得 $F'=0$ 在定义域内同样有且仅有一个解。

\[ \begin{align} f(N,x)&=f(x)=\frac{\ln(x)}{x},~f'(x)=\frac{1-\ln x}{x^2} \\F(N,x)&=f(N,x)+\frac{k}{x}, ~~F'(x)=\frac{1-\ln x-k}{x^2} \end{align} \]

易知 $f$ 有且仅有一个极值点，即 $\ln x =1$ 的时候。同时可知 $F$ 也是有且仅有一个极值点，即 $\ln x =1-k$ 的时候。因此可以使用WQS二分

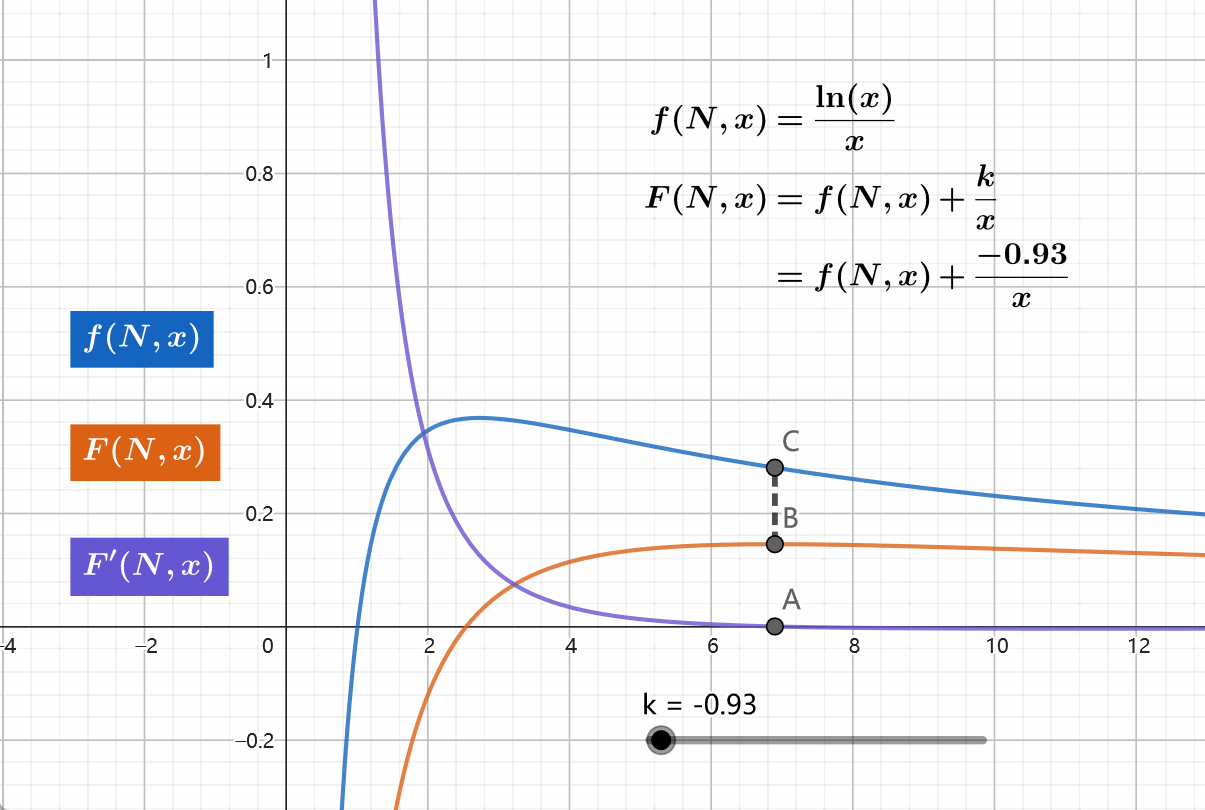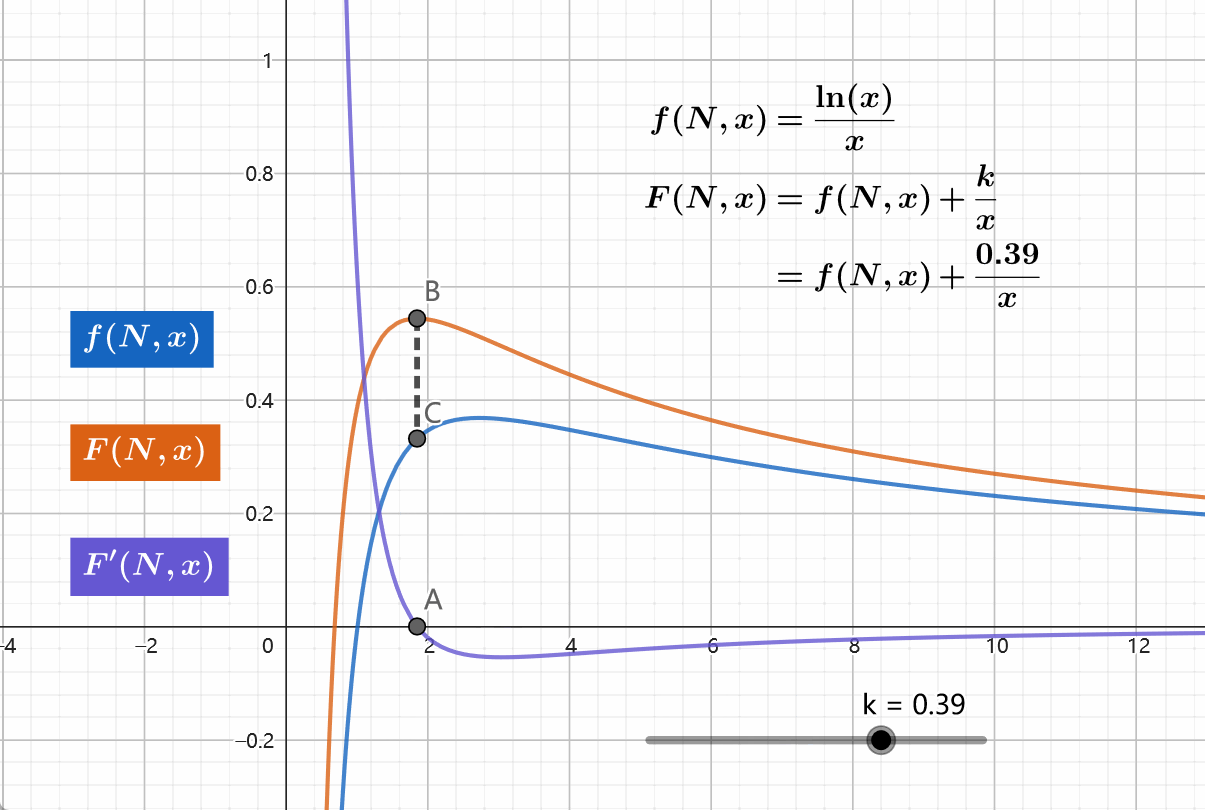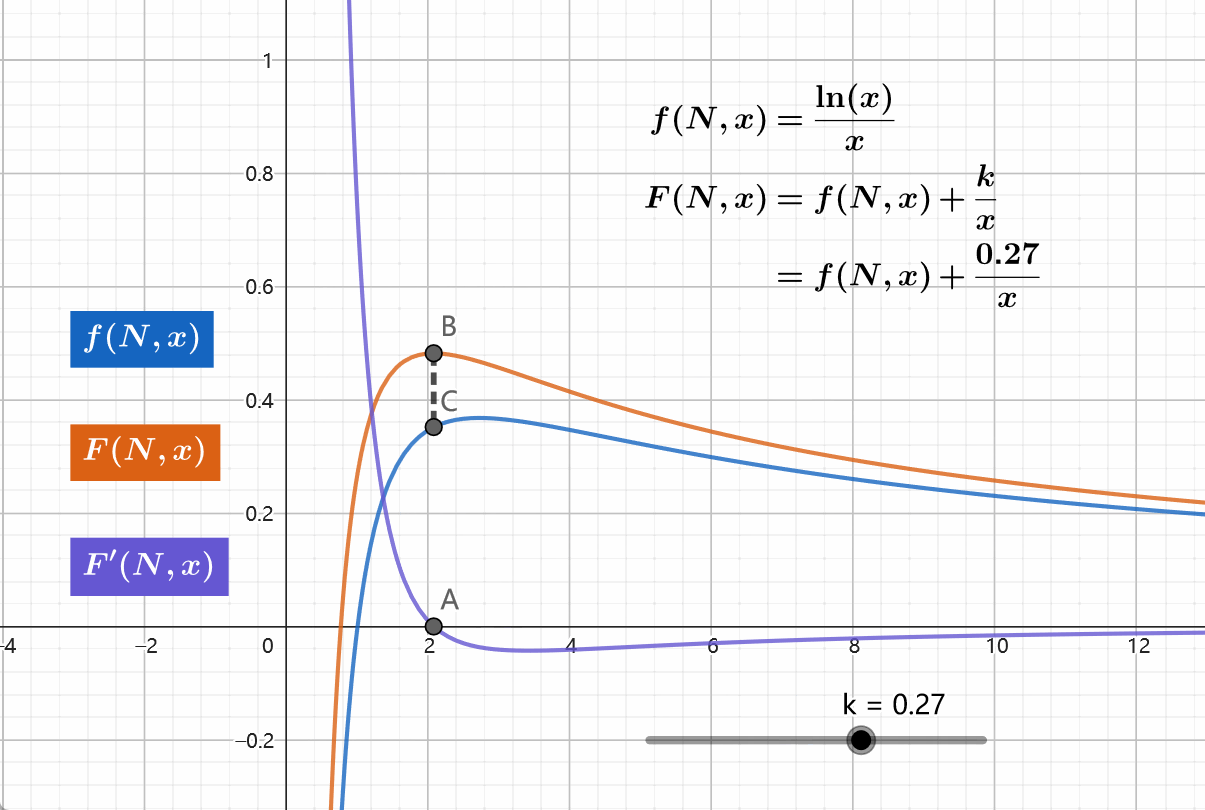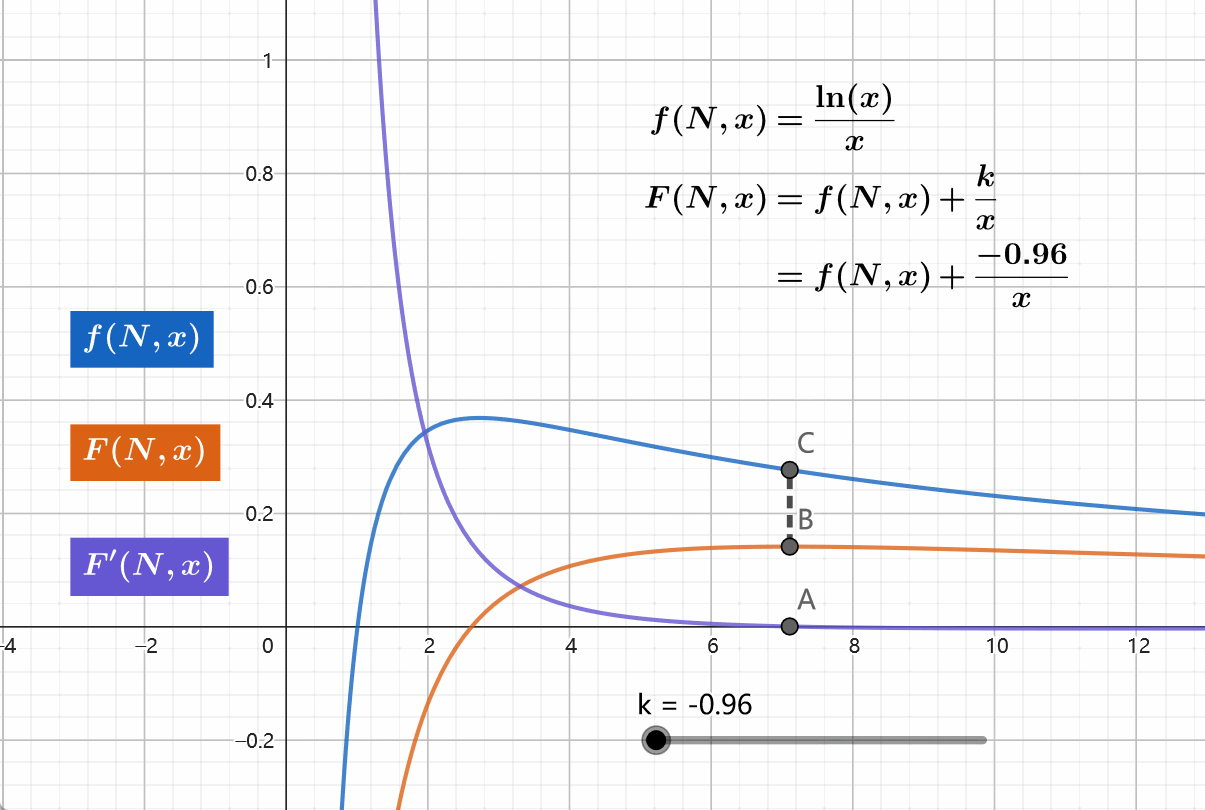
可见此方法可能在特定情境下有作用。

例二

下面 $f(x)$ 不是凸函数，考虑将其取倒数，则转变为二次函数。以此构造 $F(x)$ 。

\[ f(N,x)=f(x)=\frac{1}{x^2+1}\\ F(N,x)=F(x)=-\frac{1}{f(x)}+kx=x^2+kx+1 \]

则此时 $f(x)=\frac{1}{kx-F(x)}$ 。由 $F(N, x=不限制)$ 获得 $f(N,x)$ 的过程如下图所示：

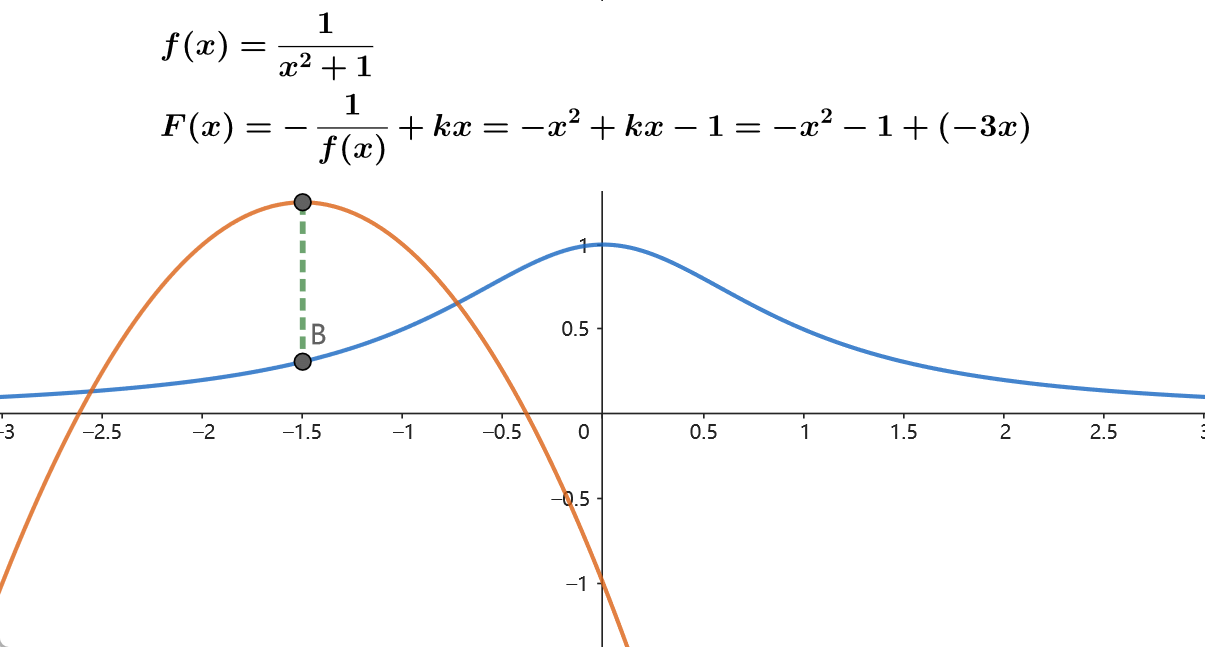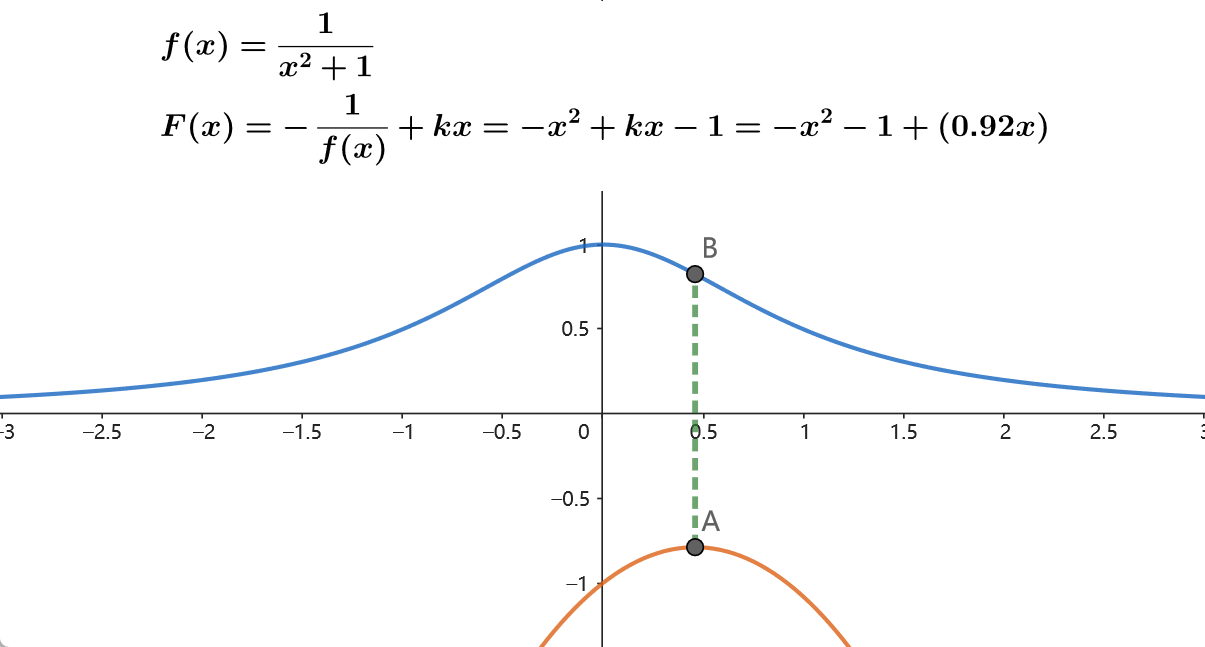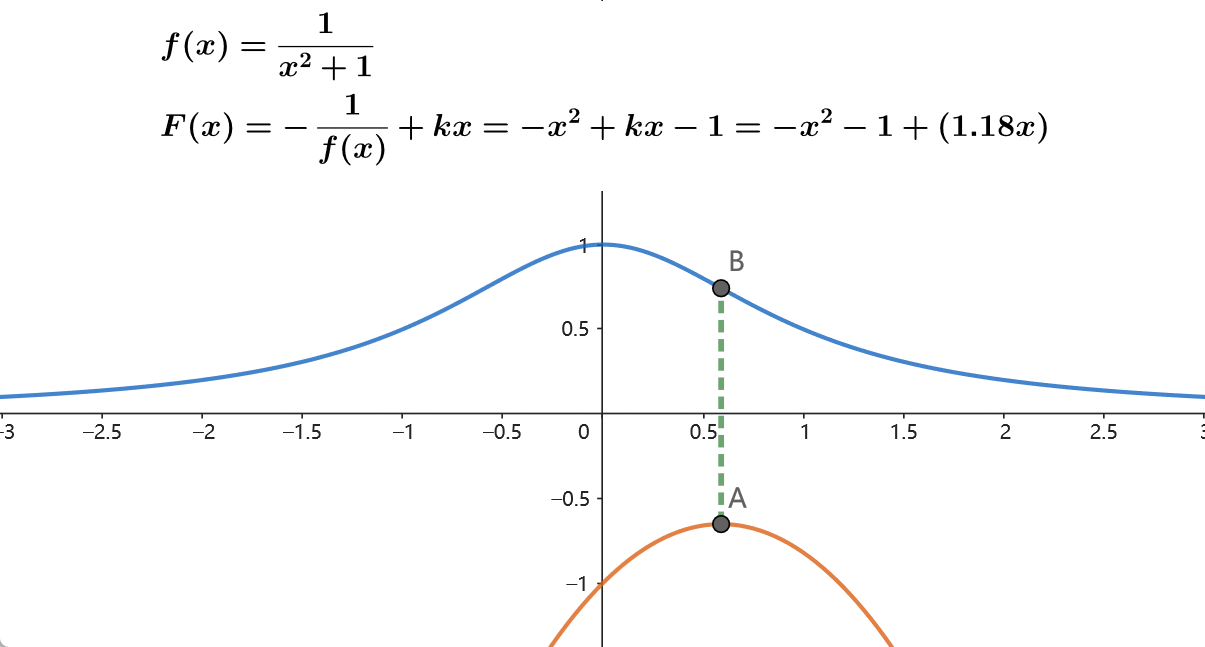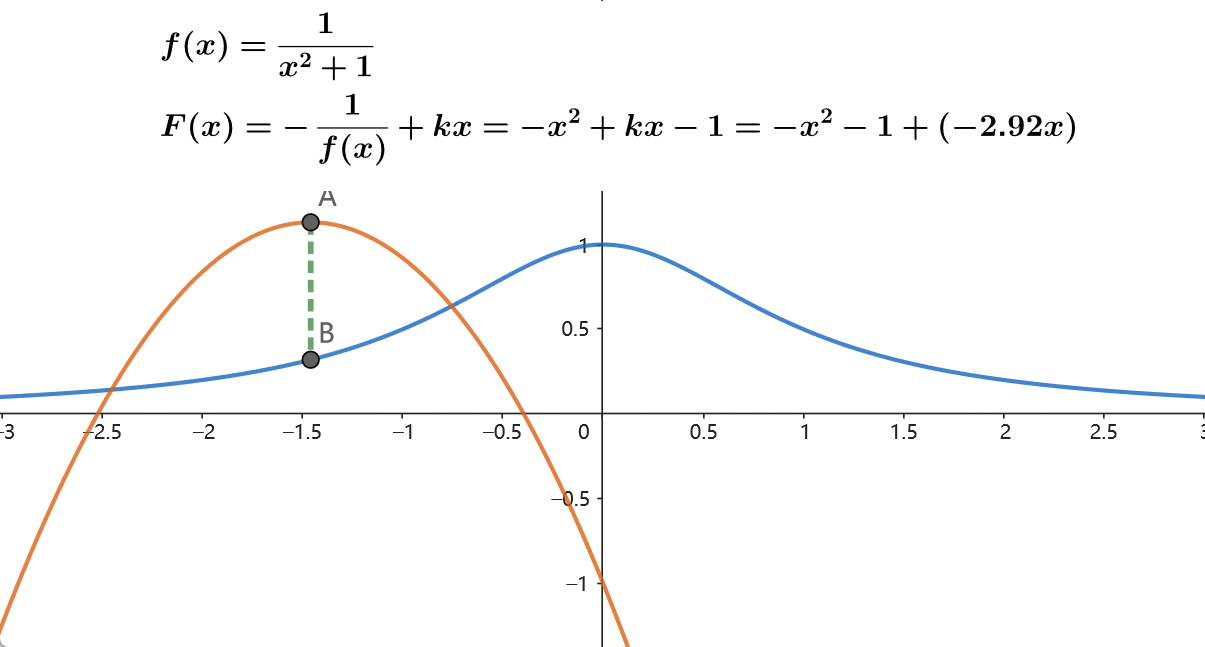
后记

以上均为连续函数，对于离散函数，比较难判断它的性质，所以感觉这个方法也没什么用。仅仅作为WQS的深入思考。也许最优化理论里面有这些研究吧。等以后学了最优化回来看看。ψ(｀∇´)ψ

要是我出WQS的题，就拿这个性质搞搞，嘻嘻~

以上就是WQS二分的详细过程与证明。

国内一般认为该算法最早由王钦石在2012年的国家集训队论文提及，故称为WQS二分。国外称为 Aliens' Trick ，源自2016年 IOI 赛题 aliens 的WQS二分解法。

WQS二分模板题

1. P4767 IOI2000 邮局

题目描述

高速公路旁边有一些村庄。高速公路表示为整数轴，每个村庄的位置用单个整数坐标标识。没有两个在同样地方的村庄。两个位置之间的距离是其整数坐标差的绝对值。

邮局将建在一些，但不一定是所有的村庄中。为了建立邮局，应选择他们建造的位置，使每个村庄与其最近的邮局之间的距离总和最小。

你要编写一个程序，已知村庄的位置和邮局的数量，计算每个村庄和最近的邮局之间所有距离的最小可能的总和。

输入格式

第一行包含两个整数：第一个是村庄 $V$ 的数量，第二个是邮局的数量 $P$。

第二行包含 $V$ 个整数。这些整数是村庄的位置。

输出格式

第一行包含一个整数$S$，它是每个村庄与其最近的邮局之间的所有距离的总和。

提示

对于 $40\%$ 的数据，$V \leq 300$。

对于 $100\%$ 的数据，$1 \leq P \leq 300$，$P \leq V \leq 3000$，$1 $ 村庄位置 $\leq 10000$。

WQS解题思路

参考博客：【ydtz】奇淫技巧——wqs二分

在分布在一条直线上的 $n$ 个村庄中选 $k$ 个建立邮局，求所有村庄到达其最近邮局的最小距离之和。$n\le 3000,k\le 300$.

这是一道四边形不等式优化 dp 的题目，但是四边形不等式好麻烦，我们不想用它 >_<

暴力的 dp 会怎么做它呢？我们通常会设 $dp_{i,j}$ 表示前 i 个村庄放 j 个邮局时的最小距离距离之和，于是有

\[ dp_{i,j}=\min(dp_{p,j-1}+w(p+1,i))\ ,\ (0\le p <i) \]

其中 $w(i,j)$ 表示的是在区间 $[i,j]$ 中建立邮局，且该区间内的村庄与该邮局的距离之和。运用一些中位数的知识，显然邮局应该建立在该区间最中间的村庄内。

这样看来 dp 转移是 $O(n^2k)$ 的，计算 $w(i,j)$ 是 $O(n)$ 的，总复杂度到达了恐怖的 $O(n^3k)$。

考虑继续优化，我们发现 $w(i,j)$ 是可以通过预处理提前求出的，由于一个区间向左右同时扩展一格时中位数不变，所以有递推式：

\[ w(i,i)=w(i+1,i)=0\\ w(i,j)=w(i+1,j-1)+a_j-a_i\ ,\ i\le j-1 \]

所以我们可以在 $O(n^2)$ 的复杂度内将 $w(i,j)$ 预处理出来，dp 的时间复杂度就优化到了 $O(n^2k)$ 。

但是仍然过不去。~~考虑继续用四边形不等式优化~~ 拒绝四边形不等式！

我们发现其实 $n^2$ 完全是能过的，只要我们能将 $k$ 优化到 $\log n$，他也是能过的。

但是单纯的 dp 显然无法做到，因为选择 $k$ 个物品这个条件所增加的状态数就足以支撑起 $O(k)$ 的时间复杂度。

这时就需要用我们的奇淫技巧——wqs 二分。

依旧设 $f(i)$ 为设立 $i$ 个邮局时的最小距离之和，则有两个性质：

$f(i)<f(i−1)$
$f(i)−f(i−1)≤f(i+1)−f(i)$

第一条十分显然，每增加一个邮局后的答案显然是不劣，主要看第二条。

第二条其实也很容易想到——每一个邮局造成影响的村庄都一定是一段区间，若后一个邮局的贡献会比前一个优，则前面显然可以先选择后一个邮局的位置建立邮局而非前一个邮局的位置，故贪心的讲，越靠前设立的邮局贡献一定越大。

通过这两条性质，我们可以很容易地推断出 $f(i)$ 的函数图像是一个下凸壳，于是就可以通过 wqs 二分将邮局个数的限制去掉，再跑 $O(n^2)$ dp 即可，时间复杂度 $O(n^2 \log |V|)$，$|V|$ 是二分的值域。

解题代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_V = 3007, MAX_P = 307;
int V, P;
int a[MAX_V], asum[MAX_V];  // a[i] 表示村庄 i 的位置，asum[i] 表示前缀和（前 i 个村庄的位置和）
// 用前缀和 O(1) 计算 w(i,j)
int W(int i, int j) {
    int mid = (i + j) >> 1;
    return (asum[j] - asum[mid]) - (asum[mid] - asum[i - 1] - a[mid] * ((i + j + 1) & 1));
}
// NOTE 这里可以用决策单调性二分队列优化为 O(nlogn)
// F(i) = min(F(j)+W(j+1,i)+k)
// 普通做法：check一次是O(n^2)，这里规定相同的消耗下，尽可能多建邮局
pair<int, int> check(int k) {
    memset(F, 0x3f, sizeof(F));
    F[0] = 0;
    for (int i = 1; i <= V; i++) {
        for (int j = 0, tmp; j < i; j++) {  // 注意j可以也必须从0开始
            tmp = F[j] + W(j + 1, i) + k;
            if (tmp <= F[i]) {
                // 尽可能少建邮局
                if (tmp == F[i]) cnt[i] = min(cnt[i], cnt[j] + 1);
                else cnt[i] = cnt[j] + 1;
                F[i] = tmp;
            }
        }
    }
    return {F[V], cnt[V]};
}
// WQS二分查找：共查找 log2(n)=log2(3e7)=25 次
void solve() {
    int l = 0, r = 3000 * 10000, mid, ans;
    while (l <= r) {
        mid = (l + r) >> 1;
        auto [Fx, cnt] = check(mid);
        if (cnt > P) {
            l = mid + 1;
        }
        else {
            // [Fx, cnt] 是第一个 >= P 的位置
            ans = F[V] - mid * P;   // ans 和它共线
            r = mid - 1;
        }
    }
    cout << ans << endl;
}
int main() {
    cin >> V >> P;
    for (int i = 1; i <= V; i++) cin >> a[i];
    sort(a + 1, a + V + 1);
    for (int i = 1; i <= V; i++) asum[i] = asum[i - 1] + a[i];
    solve();
    return 0;
}

左边是尽可能少建邮局，右边是尽可能多建邮局，它们的二分搜索和 $F$ 计算是不同的！

注意整数二分的时候，答案的计算一定是在二分循环里面的，因为考虑到共线的情况，如果要算的点在共线的线段中间，我们整数二分搜索是肯定搜不到的，必须通过端点来计算！（端点选哪一个根据你 $F$ 选择的贪心策略）

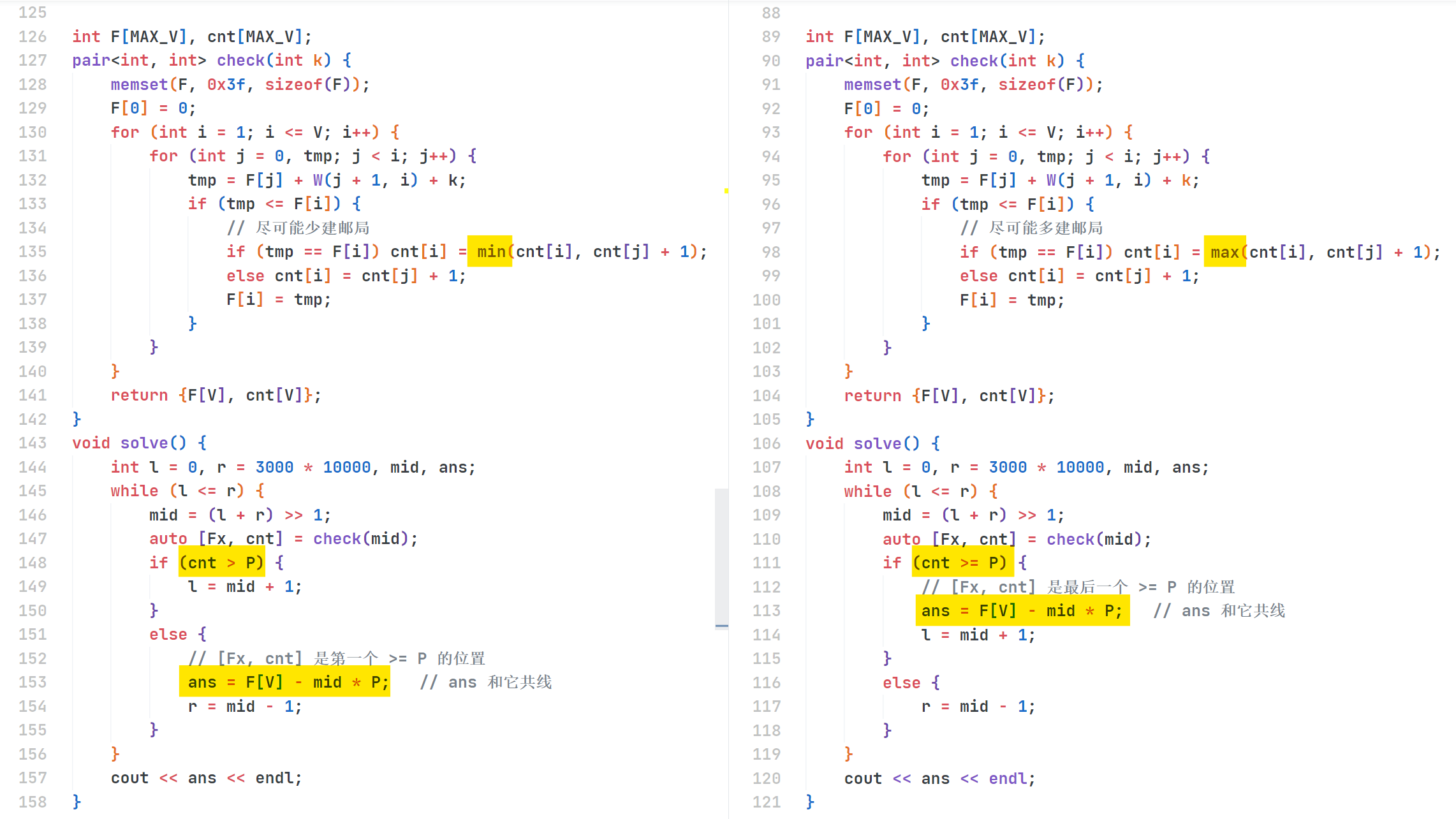
两种都能成功AC。但你要是搞错了一步就是一片的WA了！！！！虽然有的时候也能因为共线而AC。(～￣▽￣)～

2. CF739E Gosha is hunting

题目描述

你要抓神奇宝贝！现在一共有 $n$ 只神奇宝贝（ $n \le 10^5$ ）。你有 $a$ 个『宝贝球』和 $b$ 个『超级球』，其抓到第 $i$ 只神奇宝贝的概率分别是 $p_i$ 和 $q_i$ ，每种球不能在同一只神奇宝贝上使用多次。求最优策略下，抓到神奇宝贝的总个数期望最大值，保留五位小数。

WQS解题思路

这道题很好地指出了多重WQS二分是如何操作的。

设 $f(i,j,k)$ 为前 $i$ 个神奇宝贝中，用了 $j$ 个宝贝球和 $k$ 个超级球的最大期望值。

\[ \begin{align} f(i,j,k)=max\{&f(i-1,j,k),\\&f(i-1,j-1,k)+p(i),\\&f(i-1,j,k-1)+q(i),\\&f(i-1,j-1,k-1)+1-(1-p(i))(1-q(i))\} \end{align} \]

去除限制，问题简化为：n 只神奇宝贝，任意使用宝贝球和超级球

设 $f(i)$ 为前 $i$ 只神奇宝贝中，按照规则任意使用不限量宝贝球和超级球，抓到神奇宝贝的总个数期望最大值。

第 i 只不抓： $f(i)=f(i-1)$
第 i 只使用宝贝球： $f(i)=f(i-1)+p(i)$
第 i 只使用超级球： $f(i)=f(i-1)+q(i)$
第 i 只使用宝贝球和超级球： $f(i)=f(i-1)+p(i)+q(i)-p(i)q(i)$

\[ \begin{align} f(i)=\max\{ &f(i-1),\\ &f(i-1)+p(i),\\ &f(i-1)+q(i),\\ &f(i-1)+p(i)+q(i)-p(i)q(i) \} \end{align} \]

设 $F(i)=f(i)-c_aj-c_bk$ ，则：

\[ \begin{align} F(i)=\max\{ &F(i-1),\\ &F(i-1)+p(i)-c_a,\\ &F(i-1)+q(i)-c_b,\\ &F(i-1)+p(i)+q(i)-p(i)q(i)-c_a-c_b \} \end{align} \]

$c_a$ 和 $c_b$ 由两个二分搜索嵌套得到。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2007;
const double eps = 1e-8;
int n, a, b;
double p[MAXN], q[MAXN];
double F = -eps;
pair<int, int> check(double ca, double cb) {
    double prevF = 0, selnul, sela, selb, selab;
    int prevCnta = 0, prevCntb = 0, cnta, cntb;
    for (int i = 1; i <= n; i++) {
        sela   = prevF + p[i] - ca;
        selb   = prevF + q[i] - cb;
        selab  = prevF + p[i] + q[i] - p[i] * q[i] - ca - cb;
        F = max(max(prevF, sela), max(selb, selab));
        if (F - selab < eps) cnta = prevCnta + 1, cntb = prevCntb + 1;
        else if (F - selb < eps) cnta = prevCnta, cntb = prevCntb + 1;
        else if (F - sela < eps) cnta = prevCnta + 1, cntb = prevCntb;
        else cnta = prevCnta, cntb = prevCntb;
        prevF = F, prevCnta = cnta, prevCntb = cntb;
    }
    return make_pair(cnta, cntb);
}
void solve() {
    double la = 0, ra = 1, mida, lb, rb, midb;
    pair<int, int> cnt;
    while (la + eps < ra) {
        mida = (la + ra) / 2;
        lb = 0, rb = 1;
        while (lb + eps < rb) {
            midb = (lb + rb) / 2;
            cnt = check(mida, midb);
            if (cnt.second > b) lb = midb + eps;
            else if (cnt.second < b) rb = midb;
            else break;
        }
        if (cnt.first > a) la = mida + eps;
        else if (cnt.first < a) ra = mida;
        else break;
    }
    // 这里因为小数几乎不会共线，所以不考虑共线
    // 如果是整数二分则万万不可草率地放在外面计算！！！
    cout << F + mida * a + midb * b;
}
int main() {
    cin >> n >> a >> b;
    for (int i = 1; i <= n; i++) cin >> p[i];
    for (int i = 1; i <= n; i++) cin >> q[i];
    solve();
    return 0;
}

这道题很好地展示了多重WQS的代码，以及实数二分的WQS。思想和前一题邮局差不多。只要注意二分和F计算相匹配，可以轻松AC。

这里和上一题不同的是，答案的计算放在了二分循环外面，因为是实数二分，几乎不可能共线，所以最后二分出来的 $k$ 一定是等于限定值，可以直接使用。要注意二分出来的结果是哪个变量。

（WQS最容易出错的地方在于二分，因为二分本身写法多样，细节多，出错率高）

3. P2619 国家集训队 Tree I

题目描述

给你一个无向带权连通图，每条边是黑色或白色。让你求一棵最小权的恰好有 need 条白色边的生成树。

题目保证有解。

输入格式

第一行 V,E,need 分别表示点数，边数和需要的白色边数。

接下来 E 行，每行 s,t,c,col 表示这边的端点（点从 0 开始标号），边权，颜色（0 白色 1 黑色）。

输出格式

一行，表示所求生成树的边权和。

提示

对于 5% 的数据，V≤10。对于另 15% 的数据，V≤15。对于 100% 的数据，V≤5×10^4,E≤105。

所有数据边权为 [1,100] 中的正整数。

WQS解题思路

WQS

二分每次选择白色边的额外权重 k，然后求最小生成树的权重。

Kruskal

将所有边按权重从小到大排序
依次选择边，如果边的两个端点不在同一个集合中，则将这条边加入最小生成树中
直到最小生成树中有 V-1 条边
返回树中白色边的数量

WQS + Kruskal

白边和黑边分别存储，然后按照权重排序
二分每次选择白色边的额外权重 k
为每条白色边的权重加上 k
重新排序所有边（归并排序白边和黑边）
用 Kruskal 求最小生成树
返回树中白色边的数量
如果白色边的数量大于等于 need，则说明 k 太大，否则 k 太小
二分直到找到最小的 k

#include <bits/stdc++.h>
using namespace std;
const int V_MAX = 5e4 + 10, E_MAX = 1e5 + 10;
struct edge { int s, t, c, col; };
int wcnt, bcnt;
edge W[E_MAX], B[E_MAX], G[E_MAX];
int V, E, need;
int par[V_MAX];
int find(int x) { return par[x] == x ? x : par[x] = find(par[x]); }
void mergeSort(int k) {
    int wp = 0, bp = 0;
    for (int i = 0; i < E; i++) {
        if (wp < wcnt && bp < bcnt) {
            if (W[wp].c + k <= B[bp].c) G[i] = W[wp++], G[i].c += k;
            else G[i] = B[bp++];
        }
        else if (wp < wcnt) G[i] = W[wp++], G[i].c += k;
        else G[i] = B[bp++];
    }
}
pair<int, int> kruskal() {
    int val = 0, selwcnt = 0, selcnt = 0;
    for (int i = 0; i < V; i++) par[i] = i;
    for (int i = 0; i < E; i++) {
        if (selcnt == V - 1) break;
        int par_s = find(G[i].s), par_t = find(G[i].t);
        if (par_s == par_t) continue;
        par[par_s] = par_t;
        val += G[i].c;
        selwcnt += (G[i].col == 0);
        selcnt++;
    }
    return {val, selwcnt};
}
void solve() {
    int l = -100, r = 100, mid, val, cnt, ans;
    while (l <= r) {
        mid = (l + r) / 2;
        mergeSort(mid);
        tie(val, cnt) = kruskal();
        if (cnt >= need) l = mid + 1, ans = val - mid * need;
        else r = mid - 1;
    }
    cout << ans << endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> V >> E >> need;
    for (int i = 0; i < E; i++) {
        int s, t, c, col;
        cin >> s >> t >> c >> col;
        if (col) B[bcnt++] = {s, t, c, col};
        else W[wcnt++] = {s, t, c, col};
    }
    sort(W, W + wcnt, [](edge a, edge b) { return a.c < b.c; });
    sort(B, B + bcnt, [](edge a, edge b) { return a.c < b.c; });
    solve();
    return 0;
}

WQS二分练习题

P1484 种树

题意概述

数轴上有 n 个点，每个点有一个价值 a（可以为负），两个点相邻则只能选其中一个。至多选 k 个点，计算最大价值。

WQS解题思路

很简单，直接WQS干就完了：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 300007;
ll n, k;
int a[MAXN];
pair<ll, ll> check(ll C, ll& ans) {
    ll yes = a[1] - C, no = 0, yesCnt = 1, noCnt = 0;
    ll prev_yes, prev_no, prev_yesCnt, prev_noCnt;
    for (int i = 2; i <= n; i++) {
        prev_yes = yes, prev_no = no, prev_yesCnt = yesCnt, prev_noCnt = noCnt;
        yes = prev_no + a[i] - C;
        yesCnt = prev_noCnt + 1;
        no = max(prev_yes, prev_no);
        // 选择种树最多的方案
        if (prev_yes == prev_no) noCnt = max(prev_yesCnt, prev_noCnt);
        else noCnt = (prev_yes > prev_no) ? prev_yesCnt : prev_noCnt;
    }
    ll val = max(yes, no), cnt;
    if (yes == no) cnt = max(yesCnt, noCnt);
    else cnt = (yes > no) ? yesCnt : noCnt;
    return make_pair(val, cnt);
}
int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    ll l = 0, r = *max_element(a + 1, a + n + 1), mid, val, cnt, ans = -1;
    while (l <= r) {
        mid = l + ((r - l) >> 1);
        tie(val, cnt) = check(mid, ans);
        if (cnt >= k) l = mid + 1, ans = val + k * mid;
        else r = mid - 1;
    }
    // 因为 cnt 最大为树坑为非负数的个数，所以 cnt 可能恒小于 k
    if (ans == -1) ans = val + k * mid;
    cout << ans;
    return 0;
}

P5896 IOI2016 aliens

题意概述

m x m 方格中填有非负整数，其和为 n 。规定左上到右下为对角线，选择的正方形区域的对角线必须和这条对角线重合。在对角线上选择正方形区域，使得正方形能够覆盖所有不为 0 的方格，并要求被覆盖的方格数最小。现在限制最多只能选择 k 个正方形，求最小的被覆盖的方格数。

WQS解题思路

凸性。那必然拍的越多，每次降低的费用就越少。
将方格左下三角形按照对角线对称到右上，不影响结果。
将每个点的坐标视为线段区间，这根线段则是在对角线上的。作正方形区域，相当于取对角线上的一个线段区间。
排序线段。对线段按照左端点从小到大排序，相同则按照右端点降序。
删除被包含的线段。通过对比右端点（因为左右端点已有序）。
WQS二分每次拍照额外的费用 $C$ ，值域设置到题目极限状态 $[0,m^2]$ ，否则被卡。
设 $f(i)$ 为前 i 个线段所拍到的最少方格数量，则 $F(i) = f(i) + C * 拍照次数$ 。
状态转移方程：

\[ F(i) = F(j)+(r_i-l_{j+1}-1)^2-G(j)+C,\quad G(j)= \begin{align}\left\{\begin{aligned}& (r_j-l_{j+1}+1)^2,\quad r_j \ge l_{j+1} \\& 0,\quad r_j < l_{j+1}\end{aligned}\right.\end{align} \]

$G(j)$ 是新拍照区域和旧区域的重叠区域，根据是否重叠，减去重复计算的方格。
上面的式子平方项很眼熟，直接斜率优化+单调队列 $O(n)$ 解决。
最终时间复杂度为 $O\left(n\log (m^2)\right)= O(n\log m)$ 。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define MAXN 100007
struct seg {ll l, r;} a[MAXN];
ll n, m, k;
ll q[MAXN], head = 0, tail = -1;
ll F[MAXN], CNT[MAXN], C;
#define SQ(x) ((x)*(x))
#define X(j) (a[j+1].l)
#define G(j) (a[j].r>=a[j+1].l?SQ(a[j].r-a[j+1].l+1):0)
#define Y(j) (F[j]+SQ(a[j+1].l)-G(j)+C)
#define K(i) (2*(a[i].r+1))
#define B(i) (F[i]-SQ(a[i].r+1))
// 使用 <= 尽可能多拍照片
#define slope_le_k(p1,p2,k) ((Y(p1)-Y(p2))<=(X(p1)-X(p2))*(k))  
#define k1_le_k2(p1,p2,p3,p4) ((Y(p1)-Y(p2))*(X(p3)-X(p4))<=(Y(p3)-Y(p4))*(X(p1)-X(p2)))
// 斜率优化
pair<ll, ll> check() {
    head = 1, tail = 1;
    q[tail] = 0, F[0] = 0, CNT[0] = 0;
    for (int i = 1; i <= n; i++) {
        while (head < tail && slope_le_k(q[head+1], q[head], K(i))) head++;
        ll j = q[head];
        F[i] = F[j] + SQ(a[i].r-a[j+1].l+1) - G(j) + C;
        CNT[i] = CNT[j] + 1;
        while (head < tail && k1_le_k2(q[tail], i, q[tail-1], q[tail])) tail--;
        q[++tail] = i;
    }
    return make_pair(F[n], CNT[n]);
}
int main() {
    ios::sync_with_stdio(false); cin.tie(0);
    cin >> n >> m >> k;
    a[0].l = -1, a[0].r = -1;   // 非常重要，否则一开始G(0)会出错
    for (int i = 1; i <= n; i++) {
        cin >> a[i].l >> a[i].r;
        if (a[i].l > a[i].r) swap(a[i].l, a[i].r);
    };
    sort(a+1, a+n+1, [](seg _a, seg _b){return _a.l==_b.l?_a.r>_b.r:_a.l<_b.l;});

    // 去掉被包含的线段
    ll wp = 1;
    for (int i = 2, prev_r = a[1].r; i <= n; i++)
        if (prev_r < a[i].r) a[++wp] = a[i], prev_r = a[i].r;
    n = wp;

    // WQS二分
    ll lt = 0, rt = 1e12, val, cnt, ans = -1;
    if (k > n) k = n;  // 用了这个优化，就不需要下面的 if (ans == -1) 了
    while (lt <= rt) {
        C = (lt + rt) >> 1;
        tie(val, cnt) = check();
        // 在多点共线的线段上，[val, cnt] 是最后一个 >= k 的值
        if (cnt >= k) lt = C + 1, ans = val - k * C;  // [val, k] 和 [val, cnt] 共线
        else rt = C - 1;
        if (cnt == k) break;  // 非常必要的小优化
    }
    // 虽然是凸函数，但是单调不增，并且最终无论拍多少次，都会收敛到一个值。
    // 所以当 k > n 时，cnt 必然小于 k，而 k 会和 n 共线
    // if (ans == -1) ans = val - k * C;  
    cout << ans << endl;
    return 0;
}

同样对比两种不同的二分方式和F计算：

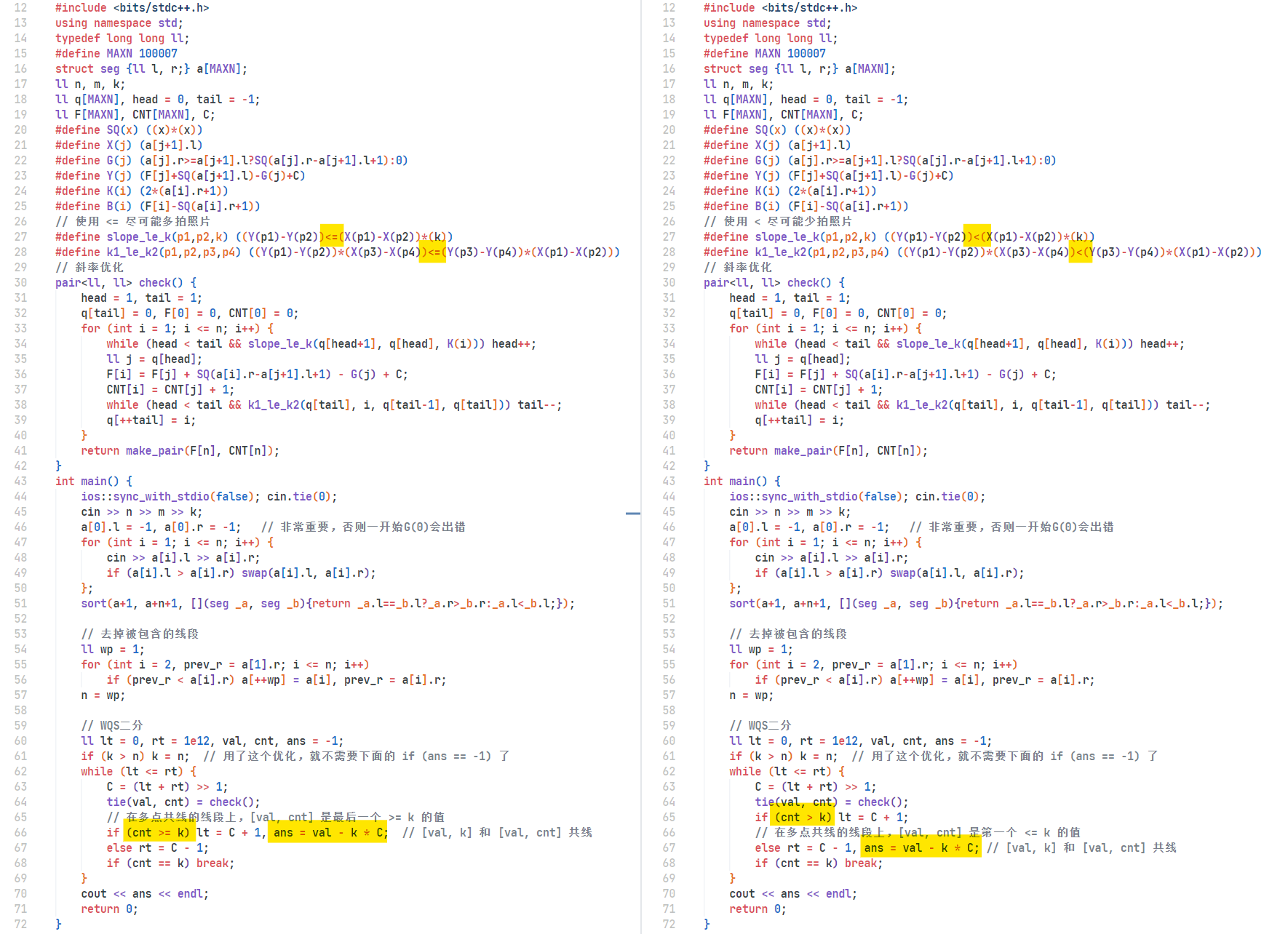
aliens对比

两种都可成功AC：

6 (2D/0D) 矩阵乘法优化

https://www.cnblogs.com/Xing-Ling/p/11594147.html

7 (1D/1D) 闵可夫斯基和优化

参考博客：

https://www.cnblogs.com/SoyTony/p/Learning_Notes_about_DP_Optimization_3.html

https://www.luogu.com.cn/blog/juefan/Minkovski-Sum#

https://www.cnblogs.com/apjifengc/p/17041194.html

概述

用于优化 $(\max/\min,+)$ 卷积，形如：

\[ f_i=\max_{j=0}^i/\min_{j=0}^i \{g_j+h_{i-j}\} \]

要求 $g,h$ 具有凸性。

计算 $g$ 和 $h$ 的差分序列，然后将两个序列进行归并排序，然后取前 $i$ 个元素。最终结果即为 $f_i$ 。

算法流程

以 $\max$ 为例，要求 $g,h$ 形成上凸包，对 $g,h$ 差分，那么 $f_i$ 相当于在 $\Delta g$ 和 $\Delta h$ 中选两个前缀，要求长度和为 $i$，权值和最大。由于 $\Delta g$ 和 $\Delta h$ 都单调不升，那么归并排序之后选前 $i$ 个数就是最优。

同理 $\min$ 要求 $g,h$ 形成下凸包。

vector<int> Minkowski(vector<int> g,vector<int> h){
    vector<int> f;
    for(int i=(int)g.size()-1;i>=1;--i) g[i]-=g[i-1];
    for(int i=(int)h.size()-1;i>=1;--i) h[i]-=h[i-1];
    f.resize(g.size()+h.size());
    merge(g.begin(),g.end(),h.begin(),h.end(),f.begin(),greater<int>());
    for(int i=1;i<f.size();++i) f[i]+=f[i-1];
    return f;
}

优化 DP

通常与分治同时使用。

转移方程形如：

\[ f_{i,j}=\max_{j=0}^i/\min_{j=0}^i\{f_{i-1,j}+w_{i,i-j}\} \]

若 $f,w$ 均具有凸性，可以使用闵可夫斯基和优化至 $O(n)$ 转移一行，改成分治求区间的 $f$ 值，每一层的总规模 $O(n)$，可以做到 $O(n\log n)$。

例题

QOJ-5421 Factories Once More

考虑树上背包，设 $f_{u,i}$ 为 $u$ 子树内选 $i$ 个节点的最大答案，转移是：

\[ f_{u,i}=\max_{j=0}^{siz_v}\{f_{u,i-j}+f_{v,j}+j(k-j)\times w(u,v)\} \]

注意到贡献函数是上凸的，转移形如 $(\max,+)$ 卷积，因此得知 $f_u$ 是上凸的，那么维护差分数组使用闵可夫斯基和优化。

需要启发式合并，维护单调不升的差分数组使用 Splay，而 $j(k-j)\times w(u,v)$ 差分后是等差数列，维护一个加等差数列的标记即可。

时间复杂度 $O(n\log n)$。

参考资料

【学习笔记】闵可夫斯基和 - APJifengc

8 (1D/1D) Slope Trick

这是一个优化凸函数合并的技巧。

这里使用的场景是：凸函数 $f$ + 凸函数 $g$ = 凸函数 $h$ （当然，他们的凸性必须相同）

概述

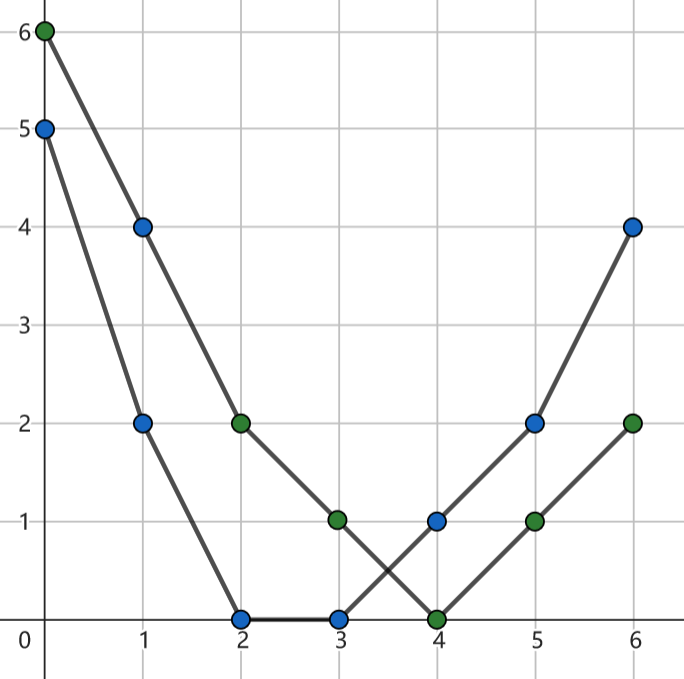
两个下凸包

如图，是两个下凸包。通常，我们保存每一个点的坐标。

然而，这种方式在合并两个凸包时是比较麻烦的：我们必须对每个下标对应的元素进行加法操作。当然这在凸包比较多转折点时还是比较合理的。

// Convex hull 1
    int ch1[7] = {5, 2, 0, 0, 1, 1 ,4};
// Convex hull 2
    int ch2[7] = {6, 4, 2, 1, 0, 1 ,2};
// All
    int ch[7] = {11, 6, 2, 1, 1, 2, 6};

现在有一种新的方法来存储凸函数：保存斜率的变化点，在这个点处，斜率增加（或减少）了多少，就存几次这个点的下标。

// Convex hull 1
    int k1 = -3, b1 = 5;
    int ch1[5] = {1, 2, 2, 3, 5};
// Convex hull 2
    int k2 = -2, b2 = 6;
    int ch2[5] = {2, 4, 4, 4, 4};
// All
    int k = -5, b = 11;
    int ch[10] = {1, 2, 2, 2, 3, 4, 4, 4, 4, 5};

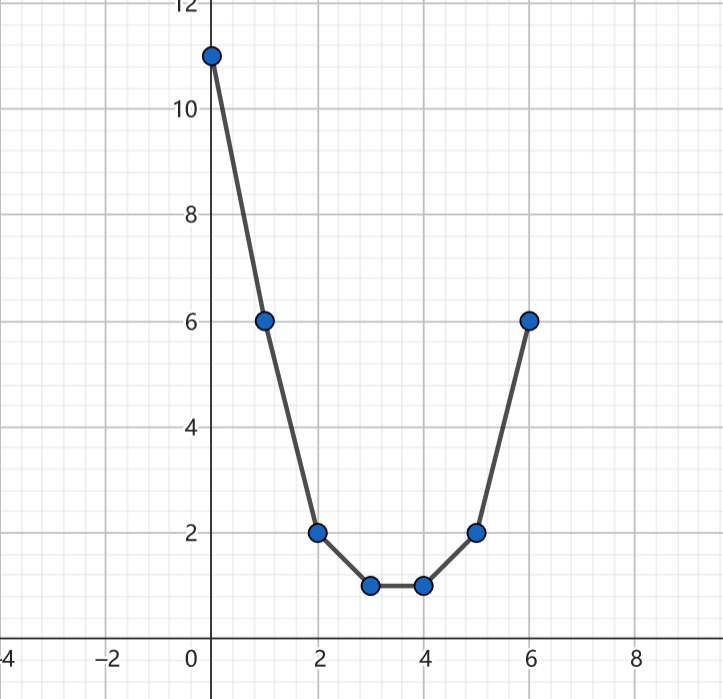
合并后的凸包

这种新方法需要将两个序列进行归并排序。

例题

1. CF713C Sonya and Problem Wihtout a Legend

题意：给定 $n$ 个正整数 $a_i$ ，每次操作可以选择任意一个数将其 $+1$ 或 $-1$ ，问至少需要多少次操作可以使得 $n$ 个数保持严格单增。

数据范围： $1 \le n \le 3000,1\le a_i\le 10^9$

解题思路

首先有一个技巧，可以将严格单增转化为单调不减。

假设 $a_i$ 为严格单增，则有 $a_i + 1 \ge a_{i-1}$ 。令 $b_i = a_i - i$ ，则有 $b_i - b_{i-1} = a_i - i - [a_{i-1} - (i-1)]=(a_i+1)-a_{i-1}\ge0$ 。所以只需要维护 $b_i$ 为单调不减即可获得严格单增的 $a_i$ 。

设 $f_{i,x}$ 为前 $i$ 个数字，第 $i$ 个数 $a_i$ 最终变为 $x$ 所需的最少总操作数。则有：

\[ f_{i,x}=\min\{\min\limits_{t\le x}\{f_{i-1, t}\} + |a_i-x|\} \] 朴素DP做法

单调不增的序列有一个定理：

...

根据这个定理进行离散化，将 $b$ 进行排序后映射到下标。设排序后的 $b$ 数组为 $bs$ 。则：

\[ f_{i,j}=\min\{\min\limits_{t\le j}\{f_{i-1, t}\} + \left|b[i]-bs[j]\right|\} \] 不过，这是从 $b[i]$ 变到 $bs[j]$ 的总最少耗费。可是为什么代码中却不用恢复减去的 $i$ 呢？

设 $ac[i]$ 为最终的严格单调序列， $bc[i]$ 为最终的单调不减序列。则：

\[ \begin{align} \min\limits_{j\le n}\{dp[n][j]\} &= \sum|bc[i]-b[i]|\\ &= \sum|(bc[i]+i)-(b[i]+i)|\\ &= \sum |ac[i]-a[i]| \end{align} \]

所以这里不需要再对结果进行什么恢复操作了，直接遍历寻找 dp[n][i] 的最小值即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f3f3fLL
ll n, m, dp[3010][3010], b[3010], bs[3010];
int main() {
    scanf("%lld", &n);
    for (ll i = 1; i <= n; i++) {
        scanf("%lld", &b[i]);
        b[i] -= i;
        bs[i] = b[i];
    }
    sort(bs + 1, bs + n + 1);
    memset(dp, INF, sizeof(dp));
    dp[0][1] = 0;
    for (ll i = 1; i <= n; i++) {
        for (ll j = 1, fmin = INF; j <= n; j++) {
            fmin = min(fmin, dp[i - 1][j]);
            dp[i][j] = fmin + abs(b[i] - bs[j]);
        }
    }
    ll nmin = INF;
    for (ll i = 1; i <= n; i++)
        nmin = min(nmin, dp[n][i]);
    cout << nmin;
    return 0;
}

Slope Trick 做法

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n, t;
    long long ans = 0;
    priority_queue<int> Q;
    scanf("%d%d", &n, &t);
    Q.push(t);
    for (int i = 1; i < n; i++) {
        scanf("%d", &t);
        t -= i;
        Q.push(t);
        if (Q.top() > t) {
            ans += Q.top() - t;
            Q.pop();
            Q.push(t);
        }
    }
    printf("%lld", ans);
    return 0;
}

9 (xD/yD) 数据结构优化

算法 > 动态规划

#DP #Algorithm 算法 #DP优化

【算法】DP优化总结

https://qalxry.github.io/2024/01/20/【算法】DP优化总结/

作者

しずり雪

发布于

2024年1月20日

更新于

2024年4月13日

许可协议

【Hexo】网站建设记录-2024年1月26日上一篇

【算法】【状压DP】最短 Hamilton 路径中被忽视的玄妙之处下一篇

【算法】DP优化总结

DP优化总结

0 基本概念

1D/1D 方程

(1) \(w(i,j)\) 为多项式函数

a. \(w(i,j)\) 为一次函数：单调队列优化

b. \(w(i,j)\) 为高次函数：斜率/凸壳优化

(2) \(w(i,j)\) 为非多项式函数

a. \(w(i,j)\) 满足四边形不等式：决策单调性优化

2D/1D 方程

(1) \(f(i,j)\) 具有凸性

(2) \(w(i,j)\) 满足四边形不等式

1 (1D/1D) 单调队列优化

概念

(1) \(ds[j]\) 与 \(i\) 无关：单调队列

(2) \(ds[j]\) 与 \(i\) 有关：二分单调栈

单调队列优化模板题

1. 【单调队列】P2627 USACO11OPEN Mowing the Lawn G

2. 【二分单调栈】

2 (1D/1D) 斜率/凸壳优化

概念

(1) \(k,x\) 同单调：单调队列

(2) \(k\) 不单调，\(x\) 单调：二分单调栈

(3) \(k\) 单调，\(x\) 不单调：动态凸包

(4) \(k\) 不单调，\(x\) 不单调：动态凸包

A. 动态凸包：李超线段树

斜率优化模板题

1. 【单调队列】Print Article HDU3507

2. 【二分单调栈】

3. 【动态凸包】

3 (1D/1D) 决策单调性优化

概念

四边形不等式的性质

a. \(\frac{\partial^2 w}{\partial y\partial x} \le 0\)

b. \(\frac{\partial^2 w}{\partial x\partial y} \le 0\)

结论与拓展

(1) 方法一：单调队列 + 二分

(2) 方法二：分治法

(3) 方法三：SMAWK 算法

(4) 方法四：Wilber 算法

(5) 方法五：Eppstein 算法

决策单调性模板题

1. 【单调队列二分】P1912 NOI2009 诗人小G

2. 【分治法】CF868F Yet Another Minimization Problem

3. 【分治法】POI2011 Lightning Conductor

决策单调性练习题

4 (2D/1D) 四边形不等式优化

概念

区间决策单调性模板题

5 (2D/1D) WQS带权二分优化

题目类型

朴素DP思路

WQS二分解题思路

1. 检查 \(f(i=C,j)\) 关于 \(j\) 的凸性

2. 简化问题：不限制 \(j\) 时的 \(f(i,j=不限制)\) 很好算

3. 凸函数：加减 \(kx\) 凸性不变，最值点单调移动

4. 加减 \(kx\) 构造新凸函数，用其最值点求 \(f(i,j)\)

5. 二分搜索合适的 \(k\) 值，得到 \(f(N,M)\)

6. 特别注意事项

(1) 注意多点共线

(2) 注意 M 是否永远无法通过二分取到

WQS二分的拓展

A. 多重WQS二分

B. 对任意凸函数中受限制变量进行二分

C. 对非凸函数进行WQS二分

WQS二分模板题

1. P4767 IOI2000 邮局

2. CF739E Gosha is hunting

3. P2619 国家集训队 Tree I

WQS二分练习题

P1484 种树

P5896 IOI2016 aliens

6 (2D/0D) 矩阵乘法优化

7 (1D/1D) 闵可夫斯基和优化

概述

算法流程

优化 DP

例题

QOJ-5421 Factories Once More

参考资料