【算法】图论汇总

本文最后更新于：2024年4月13日 晚上 20:08

图论汇总

00 前瞻

此篇汇总主要参考了《算法竞赛》和 oi-wiki 内的知识汇总。同时也是我个人的学习笔记，如果没有编写的，大概是还没去吧。

这里主要讲图上的问题，树上问题将会专门划分出一篇专题汇总（好吧其实是因为树上的问题有点多放在这里太挤了~）

Have a good time!

01 图的存储

1 邻接矩阵

适合稠密图，非常简单。

2 邻接表

使用动态数组存图，缺点是寻找指定邻居的效率较慢，不过邻居一般较少影响较小。

1
2
3
4
5
struct edge {
    int from, to, w;
    edge(int _from, int _to, int _w) : from(_from), to(_to), w(_w) {}
}
vector<edge> G[N];

3 链式前向星

使用静态数组模拟邻接表，相当于链表实现的邻接表，只不过使用数组模拟链表。

使用 -1 表示一条边尚未使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+5, M = 2e6+5;
int head[N], ecnt;
struct { int from, to, next, w; } edge[M];	// 这里的 from 其实可以省去
// 用 -1 表示空，需要init函数。如果用 0 表示空则可省去
void init() {
    for (int i = 0; i < N; ++i) head[i] = -1;       // 点的邻居列表索引初始化
    for (int i = 0; i < M; ++i) edge[i].next = -1;  // 边初始化
    ecnt = 0;                                       // 边计数器初始化
}
void addedge(int u, int v, int w) {
    edge[ecnt] = {u, v, head[u], w};
    head[u] = ecnt++;
}
int main() {
    init();
    int n, m; cin >> n >> m;
    for (int i = 0; i < m; i++) {int u, v, w; cin >> u >> v >> w; addedge(u, v, w);}
    // 遍历所有点的邻居
    for (int u = 0; u < N; u++) 
        for (int i = head[u]; ~i; i = edge[i].next)    // ~i 表示 i != -1
            printf("%d -> %d: %d\n", edge[i].from, edge[i].to, edge[i].w);
    return 0;
}

更加简洁的版本，使用 0 来表示一条边是未使用的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+5, M = 2e6+5;
int head[N], ecnt = 0;
struct { int to, next, w; } edge[M];
// 用 0 表示空
void addedge(int u, int v, int w) {
    ecnt++; // 需要确保第 0 个位置不存储边，因为 0 表示空
    edge[ecnt] = {u, v, head[u], w};
    head[u] = ecnt;
}
int main() {
    init();
    int n, m; cin >> n >> m;
    for (int i = 0; i < m; i++) {int u, v, w; cin >> u >> v >> w; addedge(u, v, w);}
    // 遍历所有点的邻居
    for (int u = 0; u < N; u++) 
        for (int i = head[u]; i > 0; i = edge[i].next)    // 0 表示空，所以当 i = 0 时退出
            printf("%d -> %d: %d\n", edge[i].from, edge[i].to, edge[i].w);
    return 0;
}

02 拓扑排序

概念

对一个有向无环图（Directed Acyclic Graph，DAG）\(G\) 进行拓扑排序，是将 \(G\) 中所有顶点排成一个线性序列，使得图中任意一对顶点 \(u\) 和 \(v\) ，若边 \(<u,v>\in E(G)\)，则 \(u\) 在线性序列中出现在 \(v\)​ 之前。

入度（Indegree）：以点 \(v\) 为终点的边的数量，称为点 \(v\) 的入度。

出度（Outdegree）：以点 \(u\) 为起点的边的数量，称为点 \(u\)​ 的出度。

点的入度和出度，体现了这个点在DAG中的先后关系或者优先级。

1 基于入度/出度的拓扑排序

原理

该算法也称为 Kahn 算法。这个方法就是从拓扑排序的定义出发，每次找到所有入度为 0 的点，将其加入拓扑排序的结果中，然后将这个点指向的点的入度减 1。重复这个过程，直到所有点都加入拓扑排序的结果中。

算法步骤（BFS实现）

  1. 统计所有点的入度；
  2. 找到所有入度为 0 的点，放入队列，作为起点（如果对这些点的顺序有要求，可以使用优先队列）；
  3. 如果队列初始就为空，说明图中有环，无法进行拓扑排序；
  4. 从队列中取出一个点，将其加入拓扑排序的结果中，然后将这个点指向的点的入度减 1；
  5. 如果这个点指向的点的入度被减为 0，将其加入队列；
  6. 重复 4、5 步骤，直到队列为空。
  7. 如果拓扑排序的结果不是 n 个点，说明有环。否则，返回拓扑排序的结果。

此处也可采用DFS实现，这个和后面的DFS不同，后面的DFS不依赖度数，这里的DFS依赖度数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
struct Edge {
    int to, w;
};
vector<Edge> G[N];
class TopoSort {
    vector<int> inDegree;
    vector<int> res;

public:
    // Method 1: BFS实现（推荐！！）
    vector<int> topoSort_BFS(vector<Edge> graph[], int n) {
        inDegree.resize(n);
        fill(inDegree.begin(), inDegree.end(), 0);
        res.clear();
        res.reserve(n);
        queue<int> q;
        for (int i = 0; i < n; i++)
            for (Edge& e : graph[i])
                inDegree[e.to]++;
        for (int i = 0; i < n; i++)
            if (inDegree[i] == 0) q.push(i);
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            res.push_back(u);
            for (Edge& e : graph[u]) {
                inDegree[e.to]--;
                if (inDegree[e.to] == 0)
                    q.push(e.to);
            }
        }
        if (res.size() != n)
            return {};
        return res;
    }
    // Method 2: DFS实现（不推荐！！直接用另外一个DFS比较好）
    vector<int> vis;
    vector<int> topoSort_DFS(const vector<Edge> graph[], int n) {
        res.clear();
        res.reserve(n);
        inDegree.resize(n);
        vis.resize(n);
        fill(vis.begin(), vis.end(), 0);
        fill(inDegree.begin(), inDegree.end(), 0);
        for (int i = 0; i < n; i++)
            for (const Edge& e : graph[i])
                inDegree[e.to]++;
        for (int i = 0; i < n; i++)
            if (inDegree[i] == 0 && !vis[i])
                dfs(graph, i);
        return res.size() == n ? res : vector<int>();
    }
private:
    void dfs(const vector<Edge> graph[], int u) {
        this->res.push_back(u);
        vis[u] = 1;
        for (const Edge& e : graph[u]) {
            inDegree[e.to]--;
        }
        for (const Edge& e : graph[u])
            if (inDegree[e.to] == 0 && !vis[e.to])
                dfs(graph, e.to);
    }
};
int main() {
    int n = 7;
    G[0].push_back({1, 0}); G[0].push_back({2, 0});
    G[1].push_back({3, 0}); G[1].push_back({4, 0});
    G[2].push_back({3, 0}); G[2].push_back({5, 0});
    G[3].push_back({6, 0}); 
    G[4].push_back({6, 0});
    G[5].push_back({6, 0});

    TopoSort ts;
    vector<int> res = ts.topoSort_BFS(G, n);
    if (res.empty())
        cout << "Cycle detected!" << endl;
    else {
        for (int i = 0; i < res.size(); i++)
            cout << res[i] << " ";
        cout << endl;
    }
    res = ts.topoSort_DFS(G, n);
    if (res.empty())
        cout << "Cycle detected!" << endl;
    else {
        for (int i = 0; i < res.size(); i++)
            cout << res[i] << " ";
        cout << endl;
    }
    return 0;
}

输出：

1
2
0 1 2 4 5 3 6 
0 1 4 2 5 3 6

2 基于DFS的拓扑排序

原理

由于DFS的原理，沿着一条路径一直搜索到末端（出度为0的点），然后才开始回退，所以它遍历的顺序天然就是拓扑排序的逆序。我们需要做的只是在DFS的基础上添加对环的处理。如果图中有环，则DFS会处理到回退边，通过检测是否存在回退边则可以判断是否有环。

而回退边，我们用三个状态描述一个节点：未访问、已访问、访问中。

  • 未访问：DFS没有经过这个点。
  • 已访问：DFS结束了对该点的邻居节点的搜索，从该点往上回退。
  • 访问中：DFS在这个点经过，正在搜索这个点的邻居节点，但是还没有从这个点回退。

如果DFS访问到一个正在访问中的节点，说明这是一个回退边，即存在环，拓扑排序无解。

算法步骤

  1. 初始化所有点的状态为未访问；
  2. 从所有未访问的点开始DFS，如果DFS返回 false ，说明有环，无解；
  3. 如果DFS返回 true ，则将结果逆序，即为拓扑排序的结果。
  4. DFS 对点 \(u\) 的操作：
    • 将 \(u\) 状态设为访问中；
    • 遍历 \(u\) 的邻居 \(v\) ，如果 \(v\) 是访问中的，返回 false ；
    • 如果 \(v\) 是未访问的，递归访问 \(v\) ；
    • 将 \(u\) 状态设为已访问。
    • 将 \(u\) 加入拓扑排序的结果。
  5. 记得逆序结果！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
struct Edge { int to, w; };
vector<Edge> G[N];
class TopoSort {
    enum NodeStatus { UNVISITED, VISITED, VISITING };
    vector<int> res;
    vector<int> status;
    bool dfs(int u) {
        status[u] = VISITING;
        for (Edge& e : G[u]) {
            if (status[e.to] == VISITING) return false;
            if (status[e.to] == UNVISITED && !dfs(e.to)) return false;
        }
        status[u] = VISITED;
        res.push_back(u);
        return true;
    }
public:
    vector<int> topoSort(vector<Edge> graph[], int n) {
        res.clear(); 
        status.resize(n);
        fill(status.begin(), status.end(), UNVISITED);
        for (int i = 0; i < n; i++) {
            if (status[i] == UNVISITED && !dfs(i)) return {};
        }
        reverse(res.begin(), res.end());
        return res;
    }
};
int main() {
    int n = 4;
    G[0].push_back({1, 0}); G[0].push_back({2, 0});
    G[1].push_back({3, 0}); G[3].push_back({2, 0});
    // G[3].push_back({0, 0});
    TopoSort ts;
    vector<int> res = ts.topoSort(G, n);
    if (res.empty()) cout << "Cycle detected!" << endl;
    for (int i = 0; i < res.size(); i++) {
        cout << res[i] << " ";
    }
    return 0;
}

3 计算所有拓扑排序

这里使用基于入度的拓扑排序，同时使用回溯法搜索所有解，所以这里采用DFS来实现。

如果输入的图有环，这里将没有输出，工作非常良好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
struct Edge { int to, w; };
vector<Edge> G[N];
class TopoSort {
    vector<int> res;
    vector<int> inDegree;
    int nodeCnt;
    void dfs(int cnt) {
        // 当前路径长度等于节点个数时，输出路径
        if (cnt == nodeCnt) {
            for (auto i : res) cout << i << " ";
            cout << endl;
            return;
        }
        for (int i = 0; i < nodeCnt; i++) {
            if (inDegree[i] != 0) continue;
            res[cnt] = i;
            inDegree[i]--;                          // 更新入度
            for (Edge& e : G[i]) inDegree[e.to]--;
            dfs(cnt + 1);                           // 递归
            inDegree[i]++;                          // 回溯
            for (Edge& e : G[i]) inDegree[e.to]++;
        }
    }
public:
    void AllTopoOrder(vector<Edge> graph[], int n) {
        nodeCnt = n;
        inDegree.resize(n);
        res.resize(n);
        fill(inDegree.begin(), inDegree.end(), 0);
        for (int i = 0; i < n; i++)
            for (Edge& e : graph[i])
                inDegree[e.to]++;
        dfs(0);
    }
};
int main() {
    int n = 7;
    G[0].push_back({1, 0}); G[0].push_back({2, 0});
    G[1].push_back({3, 0}); G[1].push_back({4, 0});
    G[2].push_back({3, 0}); G[2].push_back({5, 0});
    G[3].push_back({6, 0});
    G[4].push_back({6, 0});
    G[5].push_back({6, 0});
    TopoSort ts;
    ts.AllTopoOrder(G, n);
    return 0;
}

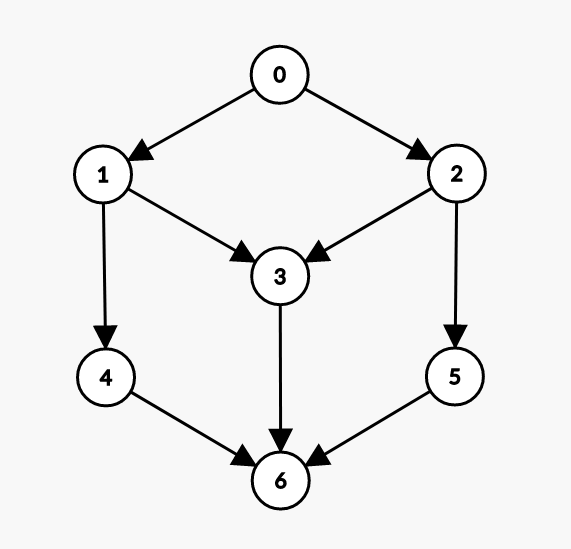
上面测试用例的DAG图：

输出的所有拓扑排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0 1 2 3 4 5 6 
0 1 2 3 5 4 6 
0 1 2 4 3 5 6 
0 1 2 4 5 3 6 
0 1 2 5 3 4 6 
0 1 2 5 4 3 6 
0 1 4 2 3 5 6 
0 1 4 2 5 3 6 
0 2 1 3 4 5 6 
0 2 1 3 5 4 6 
0 2 1 4 3 5 6 
0 2 1 4 5 3 6 
0 2 1 5 3 4 6 
0 2 1 5 4 3 6
0 2 5 1 3 4 6
0 2 5 1 4 3 6

4 计算拓扑排序的数量

统计DAG中的拓扑排序的个数等价于统计一个偏序集合上线性组合的个数，而后者是 #P-Complete 问题，没有多项式时间的算法。

或许可以用状压DP来解？暂时没有仔细想。所以，直接使用上面的算法即可。

Exploration 关于使用状压DP求解的探究

有待研究。

03 欧拉路径

概念

“一笔画”问题。

欧拉路径要求在一个图中的每条边恰好只经过一次，点可以重复经过。

  • 如果一个图中存在至少一条这样的路径，则该路径被称为欧拉路径，图被称为半欧拉图；

  • 如果这样的路径可以形成一个闭环，即起点和终点相同，则称为欧拉回路，图被称为欧拉图。

欧拉路径的存在性由图的顶点的度数（与顶点相连的边数）决定：对于无向图，若有0个或2个顶点的度数是奇数，则存在欧拉路径。

在无向图中：

  • 一个节点的度数是奇数，则称这个点为奇点。
  • 一个节点的度数是偶数，则称这个点为偶点。

1 欧拉路径和欧拉回路存在性判断

首先必须得是连通图，这个可通过并查集或者DFS判断。

无向连通图

  • 如果图中的点全部是偶点，则存在欧拉回路，任意点均可作为起点和终点。
  • 如果仅有两个奇点，则只有欧拉路，这两个奇点分别是起点和终点。
  • 其他情况，没有欧拉路。

有向连通图

  • 将一个点的一条出边记为 1 ，一条入边记为 -1，这个点的所有出度和入度相加即为这个点的度数。
  • 存在欧拉回路：当且仅当图中所有点的度数为 0 。
  • 存在欧拉路径：图中只有一个度数为 1 的点和一个度数为 -1 的点，其余的点的度数均为 0 。其中度数为 1 的点是起点，度数为 0 的点是终点。

2 输出一个欧拉回路

Hierholzer 算法（DFS 搜索）

首先需要用上述方法来判断是否有欧拉回路，

对连通图做DFS，即可输出一个欧拉回路。

  • DFS寻找到第一个无边可走的节点，则这个节点必定为终点。同时这个终点和起点是相连的。
  • 接下来由于DFS的递归回溯，会退回终点的上一个节点。
  • 继续往下搜索，直到寻找到第二个无边可走的节点，则这个节点必定为欧拉路中终点前最后访问的节点。
  • 以此类推，直到所有边都被访问。

如果是有向图，则需要用栈将DFS的输出逆序。

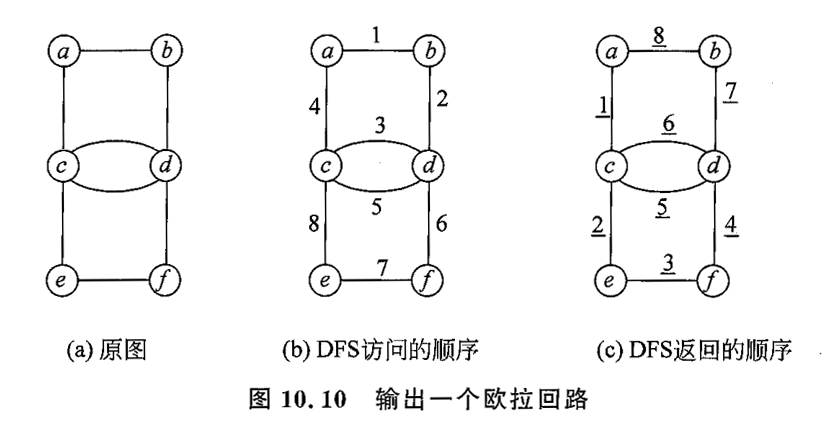
从图中可知：

  • 对于一个度数大于2的点：

    其中2个度数用于进入该点和离开该点，其余度数用于画圈（即从该点出发然后又回到该点的一条路径）。

  • 对于一个度数为2的点：

    2个度数分别用于进入该点和离开该点

注意事项

  • 不要使用邻接矩阵存图，这样在DFS遍历边的时候太慢了，时间复杂度退化为 \(O(|V||E|)\) ，应该使用邻接表存图，可以用vector或者前向星，这样时间复杂度是 \(O(|V|+|E|)\) 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
/*
Euler Path: A path that visits every edge exactly once.
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
struct Edge {
    int to, w;
};
vector<Edge> G[N];
class EulerPath {
public:
    bool hasEulerPath_Undirected(vector<Edge> graph[], int n) {
        int odd = 0;
        for (int i = 0; i < n; i++)
            if (graph[i].size() & 1) odd++;
        return odd == 0 || odd == 2;
    }
    bool hasEulerPath_Directed(vector<Edge> graph[], int n) {
        vector<int> in(n, 0), out(n, 0);
        for (int i = 0; i < n; i++)
            for (Edge& e : graph[i])
                out[i]++, in[e.to]++;
        int in0 = 0, out0 = 0;
        for (int i = 0; i < n; i++) {
            if (in[i] == out[i]) continue;
            if (in[i] - out[i] == 1)
                in0++;
            else if (out[i] - in[i] == 1)
                out0++;
            else
                return false;
        }
        return in0 == 0 && out0 == 0 || in0 == 1 && out0 == 1;
    }
    bool hasEulerCycle_Undirected(vector<Edge> graph[], int n) {
        int odd = 0;
        for (int i = 0; i < n; i++)
            if (graph[i].size() & 1) odd++;
        return odd == 0;
    }
    bool hasEulerCycle_Directed(vector<Edge> graph[], int n) {
        vector<int> in(n, 0), out(n, 0);
        for (int i = 0; i < n; i++)
            for (Edge& e : graph[i])
                out[i]++, in[e.to]++;
        for (int i = 0; i < n; i++)
            if (in[i] != out[i]) return false;
        return true;
    }
    vector<int> getEulerPath_Undirected(vector<Edge> graph[], int n) {
        path.clear();
        nodeNum = n;
        vis.clear();
        int start = 0;
        for (int i = 0; i < n; i++) {
            if (graph[i].size() & 1) {
                start = i;
                break;
            }
        }
        dfs_undirected(start, graph);
        return path;
    }
    vector<int> getEulerPath_Directed(vector<Edge> graph[], int n) {
        path.clear();
        nodeNum = n;
        vis.clear();
        vector<int> in(n, 0), out(n, 0);
        for (int i = 0; i < n; i++)
            for (Edge& e : graph[i])
                out[i]++, in[e.to]++;
        int start = 0;
        for (int i = 0; i < n; i++) {
            if (out[i] - in[i] == 1) {
                start = i;
                break;
            }
        }
        dfs_directed(start, graph);
        reverse(path.begin(), path.end());
        return path;
    }
    vector<int> getEulerCycle_Undirected(vector<Edge> graph[], int n) {
        path.clear();
        vis.clear();
        dfs_undirected(0, graph);
        return path;
    }
    vector<int> getEulerCycle_Directed(vector<Edge> graph[], int n) {
        path.clear();
        vis.clear();
        dfs_directed(0, graph);
        reverse(path.begin(), path.end());
        return path;
    }

private:
    int nodeNum = 0;
    vector<int> path;
    unordered_set<int> vis;
    inline int hash_undirected(int u, int v) {
        return min(u, v) * nodeNum + max(u, v);
    }
    inline int hash_directed(int u, int v) {
        return u * nodeNum + v;
    }
    void dfs_directed(int u, vector<Edge> graph[]) {
        for (Edge& e : graph[u]) {
            if (vis.count(hash_directed(u, e.to))) continue;
            vis.insert(hash_directed(u, e.to));
            dfs_directed(e.to, graph);
        }
        path.push_back(u);
    }
    void dfs_undirected(int u, vector<Edge> graph[]) {
        for (Edge& e : graph[u]) {
            if (vis.count(hash_undirected(u, e.to))) continue;
            vis.insert(hash_undirected(u, e.to));
            dfs_undirected(e.to, graph);
        }
        path.push_back(u);
    }
};
int main() {
    EulerPath ep;
    int n = 6;
    G[0].push_back({1, 0});
    G[1].push_back({3, 0});
    G[3].push_back({0, 0});
    G[0].push_back({2, 0});
    G[2].push_back({1, 0});
    G[1].push_back({4, 0});
    G[4].push_back({5, 0});
    G[5].push_back({2, 0});
    G[2].push_back({0, 0});
    G[3].push_back({4, 0});
    G[4].push_back({2, 0});
    G[5].push_back({3, 0});

    if (ep.hasEulerPath_Directed(G, n)) {
        vector<int> path = ep.getEulerPath_Directed(G, n);
        for (int i = 0; i < path.size(); i++)
            cout << path[i] << " ";
        cout << endl;
    }
    else
        cout << "No Euler Path\n";
    
    G[2].push_back({5, 0});
    if (ep.hasEulerCycle_Directed(G, n)) {
        vector<int> path = ep.getEulerCycle_Directed(G, n);
        for (int i = 0; i < path.size(); i++)
            cout << path[i] << " ";
        cout << endl;
    }
    else
        cout << "No Euler Cycle\n";
// =========================================
    for (int i = 0; i < n; i++)
        G[i].clear();
    G[0].push_back({1, 0});    G[1].push_back({0, 0});
    G[1].push_back({3, 0});    G[3].push_back({1, 0});
    G[3].push_back({0, 0});    G[0].push_back({3, 0});
    G[0].push_back({2, 0});    G[2].push_back({0, 0});
    G[2].push_back({1, 0});    G[1].push_back({2, 0});
    G[1].push_back({4, 0});    G[4].push_back({1, 0});
    G[4].push_back({5, 0});    G[5].push_back({4, 0});
    G[5].push_back({2, 0});    G[2].push_back({5, 0});
    G[3].push_back({4, 0});    G[4].push_back({3, 0});
    G[4].push_back({2, 0});    G[2].push_back({4, 0});
    G[5].push_back({3, 0});    G[3].push_back({5, 0});

    if (ep.hasEulerPath_Undirected(G, n)) {
        vector<int> path = ep.getEulerPath_Undirected(G, n);
        for (int i = 0; i < path.size(); i++)
            cout << path[i] << " ";
        cout << endl;
    }
    else
        cout << "No Euler Path\n";
    
    G[0].push_back({5, 0});    G[5].push_back({0, 0});
    if (ep.hasEulerCycle_Undirected(G, n)) {
        vector<int> path = ep.getEulerCycle_Undirected(G, n);
        for (int i = 0; i < path.size(); i++)
            cout << path[i] << " ";
        cout << endl;
    }
    else
        cout << "No Euler Cycle\n";

    return 0;
}

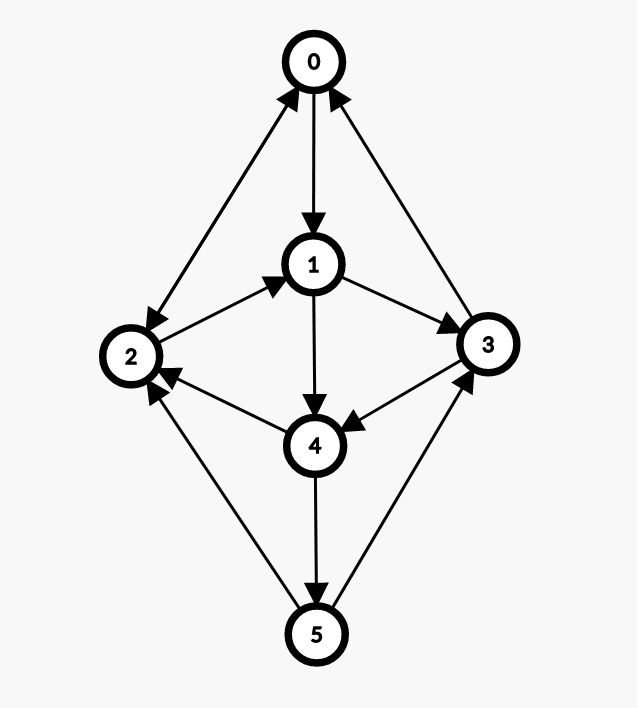
测试用例如下：

1
2
3
4
5
6
7
8
9
10
11
12
0 1
1 3
3 0
0 2
2 1
1 4
4 5
5 2
2 0
3 4
4 2
5 3

有向图后续添加了2 -> 5的边以构成回路。无向图后续添加了5 - 0的边以构成回路。

输出：

1
2
3
4
5 2 1 3 0 1 4 5 3 4 2 0 2 
0 1 3 0 2 1 4 5 2 5 3 4 2 0 
5 3 4 2 5 4 1 2 0 3 1 0 
0 5 3 4 2 5 4 1 2 0 3 1 0

Fleury 算法

该算法较不推荐，这个更适合人类来使用。

设 \(G\) 为一无向欧拉图。从一个顶点出发，走所有的边。

  • 如果这个边是当前的岛与其他岛相连的桥，则需要特别考虑：

    • 如果当前的岛内的边没有走完：不走这个桥。

    • 如果岛内的边走完了：走这个桥到其他岛。

  • 直到所有边走完。

这个如果使用编程实现，需要用反反复复用Tarjan判断桥，非常麻烦，时间复杂度也爆炸，这里就懒得实现了。这个在算法课纸质作业上用用就好。

3 混合图的欧拉路径与欧拉回路

使用到网络流内容，后续写到网络流再补充。

04 哈密顿路径

概念

  • 通过图中所有顶点一次且仅一次的通路称为哈密顿通路。
  • 通过图中所有顶点一次且仅一次的回路称为哈密顿回路。
  • 具有哈密顿回路的图称为哈密顿图。
  • 具有哈密顿通路而不具有哈密顿回路的图称为半哈密顿图。

判断一个图存不存在哈密顿回路是NP-Complete的。

性质

  • 具有3个及以上顶点的完全图是哈密顿图。
  • 正多面体是哈密顿图。
  • 大于等于二阶的竞赛图存在哈密顿路径。
  • 大于等于二阶的强连通竞赛图存在哈密顿回路。

正多面体：柏拉图立体，只有5个（正四面体、立方体、正八面体、正十二面体、正二十面体）

竞赛图：在无向完全图中为每个边缘分配方向而获得的有向图。

TODO

去看jiangly的最近的一场Div.4是怎么剪枝的。

1 获取一条哈密顿路径

可采用回溯法、分支限界法、动态规划等等方法。

（有待后续补充）

2 最短哈密顿路径（TSP问题）

概念

给定一个有权无向图，给定起点 \(0\) 和终点 \(n-1\)。求是否存在一条路径，使得每个点恰好经过一次，且路径权值和最小。

同样是NP-Hard问题，使用状压DP求解。

这里我们加强问题，改为任意起点和终点，求解全局最短哈密顿路径。

详细讲解：【算法】【状压DP】最短 Hamilton 路径中被忽视的玄妙之处

常规分析

点的编号从 \(0\) 开始到 \(n-1\) 。

用 \(dp[S][j]\) 表示点集 \(S\) 中，以 \(j\) 为终点的最短路径长度。（注意此处并没有指定起点）

我们从最小的点集开始枚举，直到逐步扩大到包含所有点的点集。最后的答案就是 \(dp[S_{final}][n-1]\)。

容易发现，\(dp[S][j]\) 的状态转移方程为：

\[ dp[S][j] = min\{dp[S-j][k] + dist[k][j]\} \quad (k \in S-j) \]

其中 \(S-j\) 表示 \(S\) 中除去 \(j\) 之外的点集。

这个状态转移方程的意思是，我们枚举 \(S-j\) 中的一个点 \(k\)，然后计算 \(dp[S-j][k] + dist[k][j]\)，即 \(S-j\) 中以 \(k\) 为终点的最短路径长度加上 \(k\) 到 \(j\) 的距离，这个值就是 \(S\) 中以 \(j\) 为终点的最短路径长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>
using namespace std;
const int N = 20;      // 最多20个点
int n, dp[1 << N][N];  // dp[S][j]表示点集S中，以j为终点的最短路径长度
int dist[N][N];        // dist[i][j]表示点i到点j的距离
int pre[1 << N][N];    // pre[S][j]记录在S中，以j为终点的前一个节点

void printPath(int S, int j) {
    stack<int> path;
    while (S) {
        path.push(j);
        int nextS = S ^ (1 << j);
        j = pre[S][j];
        S = nextS;
    }
    cout << "Path: ";
    while (!path.empty()) {
        int p = path.top();
        path.pop();
        cout << p << " ";
    }
    cout << endl;
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> dist[i][j];

    memset(dp, 0x3f, sizeof(dp));         // 初始化为无穷大
    for (int i = 0; i < n; i++) 
        dp[1 << i][i] = 0;                // 开始：集合中起点到起点的距离为0
    for (int S = 1; S < (1 << n); S++) {  // 枚举所有点集
        for (int j = 0; j < n; j++) {     // 计算在 S 中以 j 为终点的最短路径长度
            if ((S >> j) & 1) {           // S 中必须包含点 j
                for (int k = 0; k < n; k++) {     // 取出 S-j 中的一个点 k，通过枚举
                    if ((S ^ (1 << j)) >> k & 1) {  // 判断 S-j 中是否包含点 k
                        if (dp[S][j] > dp[S ^ (1 << j)][k] + dist[k][j]) {
                            dp[S][j] = dp[S ^ (1 << j)][k] + dist[k][j];
                            pre[S][j] = k;  // 记录前一个节点
                        }
                    }
                }
            }
        }
    }
    int ans = INT_MAX;
    int ans_idx = -1;
    for (int i = 0; i < n; i++) {
        if (ans > dp[(1 << n) - 1][i]) {
            ans = dp[(1 << n) - 1][i];
            ans_idx = i;
        }
    }
    cout << "Shortest Hamilton Path length: " << ans << endl;
    printPath((1 << n) - 1, ans_idx);
    return 0;
}

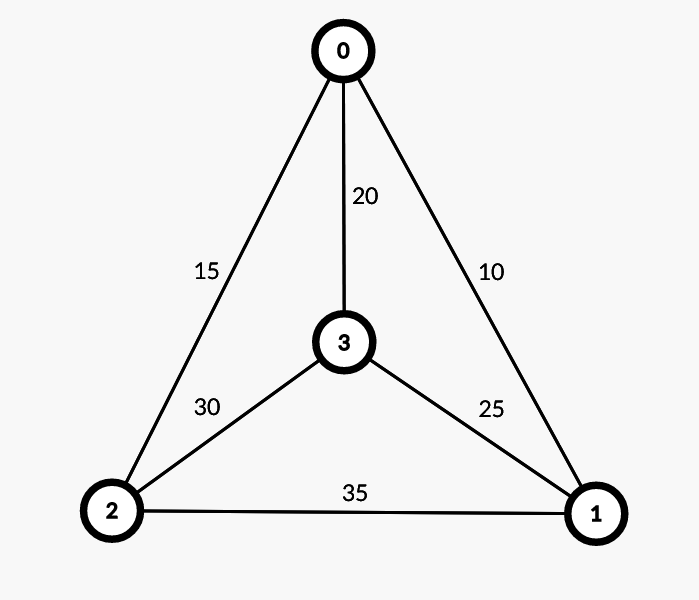
测试数据：

1
2
3
4
5
4
0 10 15 20
10 0 35 25
15 35 0 30
20 25 30 0

结果：

1
2
Shortest Hamilton Path length: 50
Path: 3 1 0 2

可见代码正确。

05 无向图的连通性

06 有向图的连通性

Kosaraju 算法

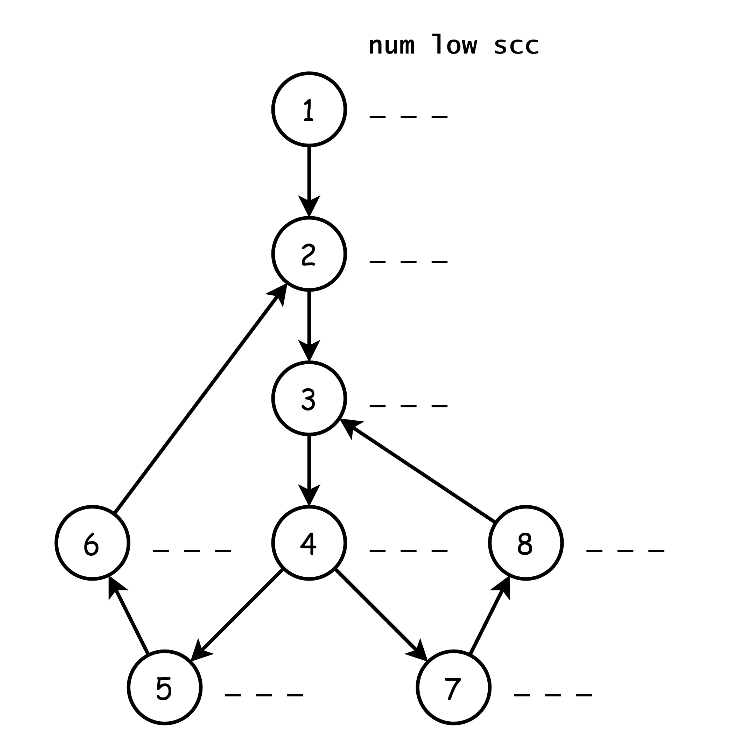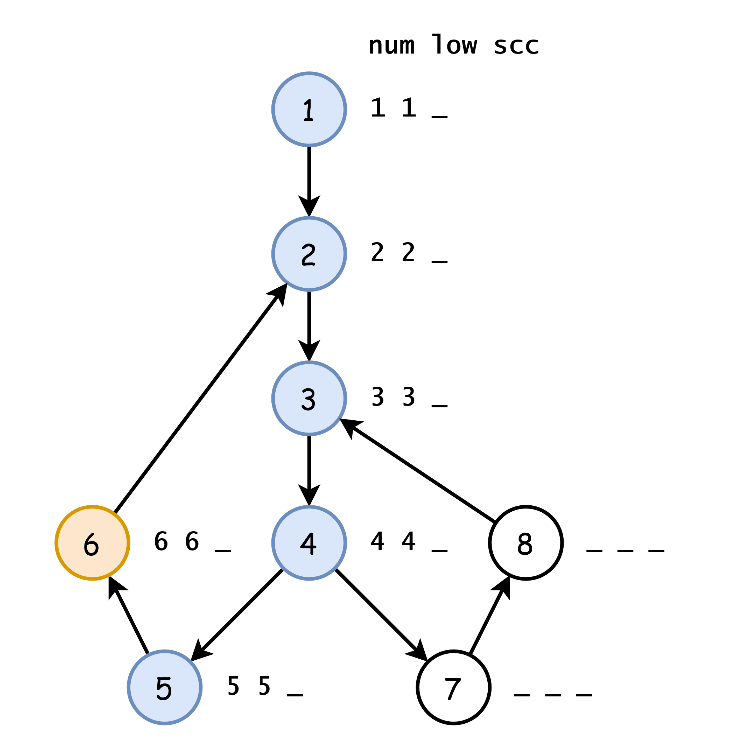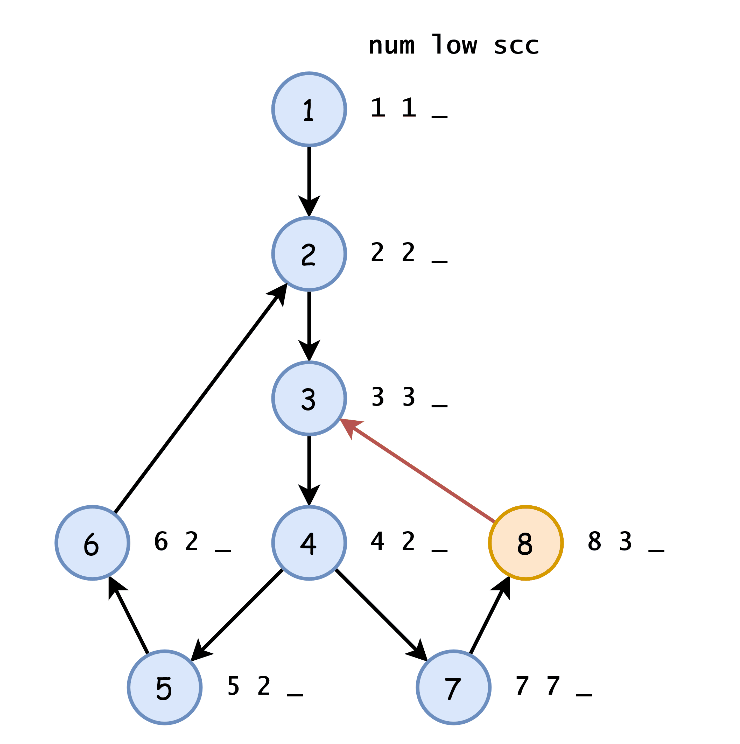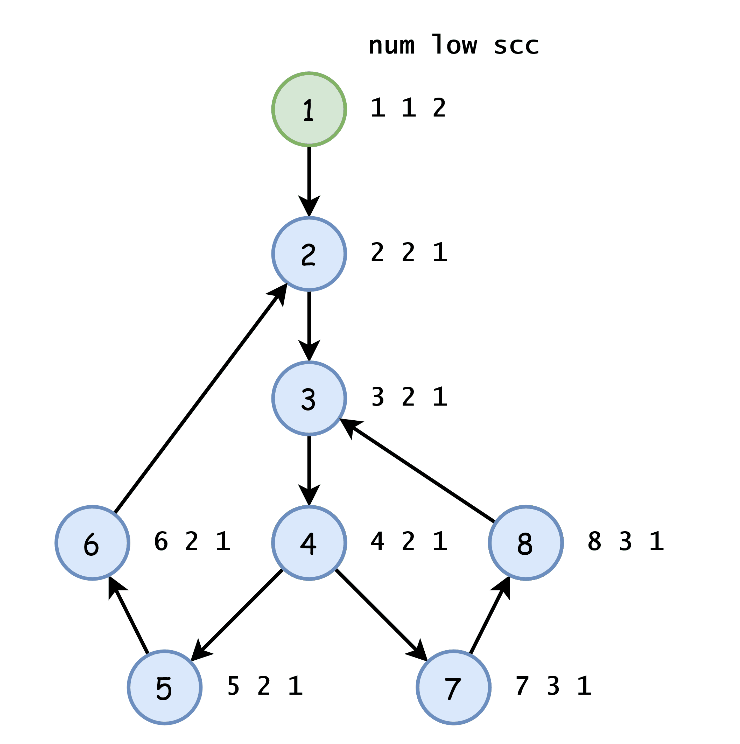
Tarjan 算法

07 基环树

08 2-SAT 问题

概念

2-SAT搜索过程与num、low、scc的确定

2-SAT 模板题

1. P4782 【模板】2-SAT

题目描述

有 \(n\) 个布尔变量 \(x_1\)\(\sim\)\(x_n\)，另有 \(m\) 个需要满足的条件，每个条件的形式都是 「\(x_i\) 为 true / false 或 \(x_j\) 为 true / false」。比如 「\(x_1\) 为真或 \(x_3\) 为假」、「\(x_7\) 为假或 \(x_2\) 为假」。

2-SAT 问题的目标是给每个变量赋值使得所有条件得到满足。

输入格式

第一行两个整数 \(n\) 和 \(m\)，意义如题面所述。

接下来 \(m\) 行每行 \(4\) 个整数 \(i\), \(a\), \(j\), \(b\)，表示 「\(x_i\) 为 \(a\) 或 \(x_j\) 为 \(b\)」(\(a, b\in \{0,1\}\))

输出格式

如无解，输出 IMPOSSIBLE；否则输出 POSSIBLE。

下一行 \(n\) 个整数 \(x_1\sim x_n\)（\(x_i\in\{0,1\}\)），表示构造出的解。

解题思路

2SAT 模板题，没什么好说的。这里 IO 比较大，用快读快写可以比关同步的 iostream 快 5 倍之多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
// 链式前向星存边
int cur, head[N << 1];
struct { int to, next; } edge[N << 2];
void addedge(int u, int v) {
    edge[++cur].to = v;
    edge[cur].next = head[u];
    head[u] = cur;
}
int low[N << 1], num[N << 1], st[N << 1], sccno[N << 1], dfn, top, cnt;
int n, m;
void tarjan(int u) {
    st[top++] = u;
    low[u] = num[u] = ++dfn;
    for (int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].to;
        if (!num[v]) {  // 没有访问过 v 点，那么递归访问 v 点
            tarjan(v);
            low[u] = min(low[u], low[v]);  // 回溯时更新 u 点的 low 值
        }
        // 访问过 v 点，但是 v 点还没有被收缩，那么更新 u 点的 low 值
        else if (!sccno[v])
            low[u] = min(low[u], num[v]);
    }
    if (low[u] == num[u]) {
        cnt++;
        while (1) {
            int v = st[--top];  // 栈顶元素出栈
            sccno[v] = cnt;
            if (u == v) break;  // 回退到了 u 点自己，退出
        }
    }
}
bool twoSAT() {
    for (int i = 1; i <= n * 2; i++)
        if (!num[i]) tarjan(i);  // 未访问过的点进行 tarjan
    for (int i = 1; i <= n; i++) {
        // a 和 !a 在同一个强连通分量中, 无解
        if (sccno[i] == sccno[i + n]) return false;
    }
    return true;
}
int main() {
    cin >> n >> m;
    while (m--) {
        int ai, a, bi, b;
        cin >> ai >> a >> bi >> b;
        int nota = a ^ 1, notb = b ^ 1;  // a 的非, b 的非
        addedge(ai + nota * n, bi + b * n);  // !a -> b
        addedge(bi + notb * n, ai + a * n);  // !b -> a
    }
    if (twoSAT()) {
        cout << "POSSIBLE" << endl;
        for (int i = 1; i <= n; i++)
            cout << (sccno[i] > sccno[i + n]) << " ";
    }
    else cout << "IMPOSSIBLE";
    return 0;
}

09 圆方树

10 最短路径问题

Floyd

Dijkstra

优化1：优先队列优化

优化2：线段树优化

https://www.cnblogs.com/ljt12138/p/6684387.html

https://www.cnblogs.com/ljt12138/p/6684387.html

zkw线段树作为小根堆来优化，比优先队列要快。

https://www.mina.moe/archives/2866

https://cc.bingj.com/cache.aspx?q=%e7%ba%bf%e6%ae%b5%e6%a0%91%e4%bc%98%e5%8c%96dijkstra&d=4930107439588083&mkt=zh-CN&setlang=zh-CN&w=auyqbo1wJQjB9Dyxy_eHVlgY90CozbU-

啊，就是我们用线段树维护 dis 数组 dis[i]表示起点到点 i的最短距离 迪杰斯特拉就是每次取出最小的 dis[i],i∈[1,n]且 i没有被选择过对吧 所以我们用线段树保存一下区间最小值。 每次取出区间 [1,n]中 dis最小的点，作为当前节点。 根据迪杰斯特拉的思想，当前节点的 dis已经最小，不可改变。 所以由当前节点扩展开来，更新与当前节点相连接的点的 dis（就是松弛操作，如果从当前节点走到下一个点，能使下一个点的 dis减少，那就从当前节点走到下一个节点） 然后在线段树中把当前节点位置的值改成 +∞，这样下次在线段树中找 min(dis)就不会再找到当前节点了（相当于堆优化中的在堆中 pop 当前节点） 然后一直循环 n次，因为一共 n个节点，每个节点会作为当前节点 1次 最后就得到了 dis数组啦，就做完迪杰斯特拉的过程了 QvQ

Bellman-Ford

Bellman-Ford算法是单元最短路径算法，即求一个起点到其他所有点的最短路径。

计算原理：

  • 一个有n个点的图
  • 给每个点n次机会，查询此时经过某个邻居是否有到起点s的更短路径，如果有则更新
  • 经过n轮查询和更新，就得到了所有点到起点s的最短路径

时间复杂度：\(O(|V||E|)\)​

能够计算含有负边的图，但下面的代码需要在print_path添加额外判断才能得知有负环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e6;
const int N = 105;
// 由于 bellman_ford 不用搜索邻居，而是直接遍历所有边
// 所以这里直接存所有边即可
struct Edge {
    int from, to, w;
} e[10005];
int n, m, cnt;
int pre[N];  // 用于记录路径
// 如果有负环，则这个print_path需要增加vis来判断路径是否循环
void print_path(int s, int t) {
    if (s == t) {
        cout << s << " ";
        return;
    }
    print_path(s, pre[t]);
    cout << t << " ";
}
// 注意这里实现的是点id从1开始的版本，要改也很简单
void bellman_ford(int s = 1, int t = n) {
    int d[N];
    for (int i = 1; i <= n; i++)
        d[i] = INF;
    d[s] = 0;
    for (int k = 1; k <= n; k++) {
        for (int i = 0; i < cnt; i++) {
            int from = e[i].from, to = e[i].to, w = e[i].w;
            if (d[to] > d[from] + w) {
                d[to] = d[from] + w;
                pre[to] = from;
            }
        }
    }
    cout << d[t] << '\n';
    print_path(s, t);
}
int main() {
    while (cin >> n >> m) {
        if (n == 0 && m == 0) return 0;
        cnt = 0;
        while (m--) {
            int u, v, w;
            cin >> u >> v >> w;
            e[cnt].from = u, e[cnt].to = v, e[cnt].w = w;
            cnt++;
            // e[cnt].from = v, e[cnt].to = u, e[cnt].w = w;
            // cnt++;
        }
        bellman_ford();
    }
    return 0;
}

SPFA

SPFA是Bellman-Ford的改进版本。

改进思路很简单：每一轮都有没有变化的点，它们不需要更新它们的邻居。这里就可以用队列来处理。

SPFA通常和Dijkstra一样快甚至更好，但是能够被刻意构造数据以达到最差时间复杂度\(O(|V||E|)\)，有的题目会故意卡SPFA。

SPFA算法步骤：

  1. 起点s入队
  2. 弹出队首元素u，更新它所有邻居的状态（从起点到u，u再到邻居）。将有变化的邻居入队。
  3. 持续以上过程，直到队列为空。

负环的判断：

  • 添加一个数组neq[N]来记录每个点入队的次数，如果入队次数大于n次，则出现了负环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 5, M = 2e6 + 5;
int n, m;
int pre[N];
void print_path(int s, int t) {
    if (s == t) {
        cout << s << ' ';
        return;
    }
    print_path(s, pre[t]);
    cout << t << ' ';
}
// 链式前向星存图
int head[N], cnt;
struct Edge {
    int to, next, w;
} edge[M];
void init() {
    for (int i = 0; i < N; ++i)
        head[i] = -1;
    for (int i = 0; i < M; ++i)
        edge[i].next = -1;
    cnt = 0;
}
void addedge(int u, int v, int w) {
    edge[cnt] = {v, head[u], w};
    head[u] = cnt++;
}
// SPFA
int dis[N];        // 记录起点到每个点的最短距离
bool inQ[N];       // 判断邻居是否存在队列中，如果存在，这里只需要修改值即可，不要重复入队
int pushTimes[N];  // 记录每个点入队的次数，如果大于n次则有负环
int spfa(int s) {
    memset(pushTimes, 0, sizeof(pushTimes));
    for (int i = 1; i <= n; i++)
        dis[i] = INF, inQ[i] = false;
    queue<int> q;
    q.push(s);
    pushTimes[s] = 1, dis[s] = 0, inQ[s] = true;
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        inQ[u] = false;  // 出队
        for (int i = head[u]; ~i; i = edge[i].next) {
            int to = edge[i].to, w = edge[i].w;
            if (dis[to] > dis[u] + w) {
                dis[to] = dis[u] + w;
                pre[to] = u;
                // 如果邻居不在队列中，则入队
                // 这样保证每轮最多只入队一次，避免重复入队
                if (!inQ[to]) {
                    inQ[to] = true;
                    q.push(to);
                    pushTimes[to]++;
                    if (pushTimes[to] > n) return 1;
                }
            }
        }
    }
    return 0;
}
int main() {
    while (cin >> n >> m) {
        init();
        if (n == 0 && m == 0) return 0;
        while (m--) {
            int u, v, w;
            cin >> u >> v >> w;
            addedge(u, v, w);
            addedge(v, u, w);
        }
        int res = spfa(1);
        if (res) {
            cout << "Have negative circle\n";
        }
        else {
            cout << dis[n] << '\n';
            print_path(1, n);
            cout << '\n';
        }
    }
    return 0;
}

SPFA优化1：SLF优化

SPFA优化2：LLL优化

11 同余最短路

12 最小生成树

13 最小直径生成树

14 最小树形图

15 最小斯纳坦树

16 网络流

17 二分图

18 图着色问题

19 图匹配问题

20 弦图

21 最大团搜索

算法 > 图论
#Algorithm 算法 #图论
【算法】图论汇总
https://qalxry.github.io/2024/03/08/【算法】图论汇总/
作者
しずり雪
发布于
2024年3月8日
更新于
2024年4月13日
许可协议