【算法】计算除数函数的和

计算除数函数 \(\sigma_{0}(n)\) 求和： \[ T(n) =\sum_{i=1}^{n} \sigma_{0}(i) =\sum_{i=1}^{n}\sum_{d~|~i}1 \] 注意到 \(\sum_{i=1}^{n}\sum_{d~|~i}1\) 代表计算 \(1\) 到 \(n\) 的所有数的约数个数之和，则可以转变思路，对于每个约数 \(d\in [1,n]\) ，计算 \([1,n]\) 中具有约数 \(d\) 的个数，对此结果进行求和即可等价于原问题： \[ \sum_{i=1}^{n}\sum_{d~|~i}1 = \sum_{d=1}^{n} \left\lfloor \frac{n}{d} \right\rfloor\le\sum_{d=1}^{n} \frac{n}{d}=n\sum_{d=1}^{n}\frac1d=nH(n) \] 其中 \(H(n)\) 为调和级数： \[ H(n)=\sum_{i=1}^{n}\frac{1}{i} \]

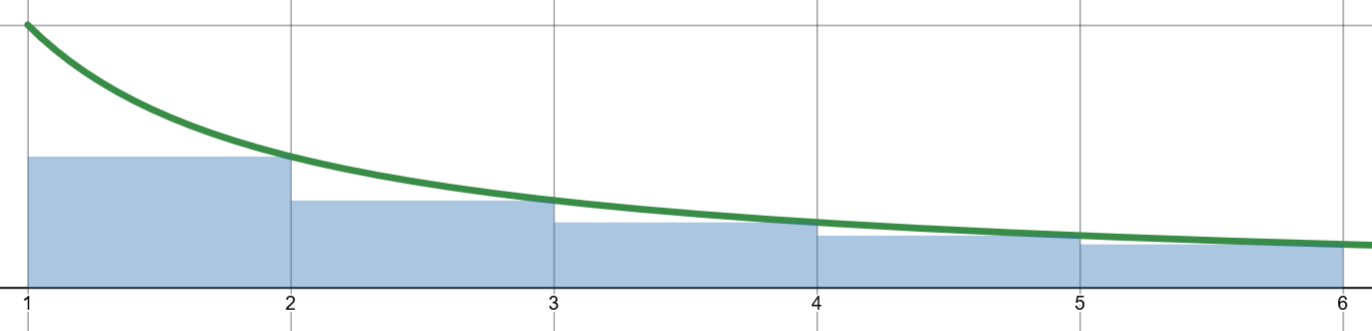
考虑构造调和级数的上界函数来计算调和级数的渐进上界。

注意到 \(H(n)-1\) 绘制为矩形并向左平移 0.5 后具有上界 \(\frac1x\) ，则通过积分计算可得： \[ H(n)-1=\sum_{i=2}^{n}\frac{1}{i} < \int_{1}^{n}\frac{1}{x}dx=\log n \]

因此时间复杂度为： \[ T(n) =\sum_{i=1}^{n} \sigma_{0}(i) =\sum_{i=1}^{n}\sum_{d~|~i}1 =\sum_{d=1}^{n} \left\lfloor \frac{n}{d} \right\rfloor \le \sum_{d=1}^{n} \frac{n}{d} =nH(n) < n(\log n + 1) = O(n\log n) \]